Self-Attention Mechanism
A Self-Attention Mechanism is a scaled dot-product attention mechanism that allows gating/multiplicative interactions between input tokens.
- AKA: Intra-Attention Mechanism, Neural Network Self-Attention Model.
- Context:
- It can be implemented in a encoder-decoder neural networks for solving machine translation tasks.
- It can be mathematically expressed in terms of self-attention weight matrix and which usually calculated using a self-attention activation function.
- ...
- Example(s)
- Decoder Self-Attention Mechanism: In machine translation, it helps align words in the source and target sentences by weighting their relationships appropriately.
- Encoder Self-Attention Mechanism: In a sentiment analysis task, the mechanism helps determine how words like "not" influence nearby adjectives, modifying their sentiment accordingly.
- Multi-headed Self-Attention Mechanism: In a mathematical formulation, the attention score is calculated as a dot product of the query and key vectors, scaled by the square root of the dimension size.
- Relation-Aware Self-Attention Mechanism: In a language model, the mechanism helps retain the meaning of words across long distances in text, improving coherence and contextuality.
- Stacked Self-Attention Mechanism: In transformer-based neural networks, multiple self-attention heads allow the model to focus on various aspects of input tokens simultaneously, enhancing its ability to understand complex patterns.
- One that is being used in BERT (Bidirectional Encoder Representations from Transformers) to capture deep bidirectional context in text.
- …
- Counter-Example(s):
- See: Self-Attention Activation Function, Transformer Network, Seq2Seq Encoder-Decoder Neural Network, Feed-Forward Neural Network, Word Embedding, Context-based Attention Mechanism, Encoder-Decoder Neural Network Attention Mechanism, Neural Machine Translation System, Statistical Machine Translation System.
References
2020a
- (GeeksforGeeks) ⇒ https://www.geeksforgeeks.org/self-attention-in-nlp/ Last Updated : 05 Sep, 2020.
- QUOTE: Self-attention was proposed by researchers at Google Research and Google Brain. It was proposed due to challenges faced by encoder-decoder in dealing with long sequences. (...)
The attention mechanism allows output to focus attention on input while producing output while the self-attention model allows inputs to interact with each other (i.e calculate attention of all other inputs wrt one input.
- QUOTE: Self-attention was proposed by researchers at Google Research and Google Brain. It was proposed due to challenges faced by encoder-decoder in dealing with long sequences.
- The first step is multiplying each of the encoder input vectors with three weights matrices $(W(Q), W(K), W(V))$ that we trained during the training process. This matrix multiplication will give us three vectors for each of the input vector: the key vector, the query vector, and the value vector.
- The second step in calculating self-attention is to multiply the Query vector of the current input with the key vectors from other inputs.
- In the third step, we will divide the score by square root of dimensions of the key vector ($d_k$)(...)
- In the fourth step, we will apply the softmax function on all self-attention scores we calculated wrt the query word (here first word).
- In the fifth step, we multiply the value vector on the vector we calculated in the previous step.
- In the final step, we sum up the weighted value vectors that we got in the previous step, this will give us the self-attention output for the given word.
- The above procedure is applied to all the input sequences. Mathematically, the self-attention matrix for input matrices $(Q, K, V)$ is calculated as: $Attention\left(Q,K,V\right)=softmax\left(\dfrac{QK^T}{\sqrt{d_k}}\right)V$where $Q$, $K$, $V$ are the concatenation of query, key, and value vectors.
2020b
- (Wikipedia, 2020) ⇒ https://en.wikipedia.org/wiki/Transformer_(machine_learning_model)#Encoder Retrieved:2020-9-15.
- Each encoder consists of two major components: a self-attention mechanism and a feed-forward neural network. The self-attention mechanism takes in a set of input encodings from the previous encoder and weighs their relevance to each other to generate a set of output encodings. The feed-forward neural network then further processes each output encoding individually. These output encodings are finally passed to the next encoder as its input, as well as the decoders.
The first encoder takes positional information and embeddings of the input sequence as its input, rather than encodings. The positional information is necessary for the Transformer to make use of the order of the sequence, because no other part of the Transformer makes use of this.
- Each encoder consists of two major components: a self-attention mechanism and a feed-forward neural network. The self-attention mechanism takes in a set of input encodings from the previous encoder and weighs their relevance to each other to generate a set of output encodings. The feed-forward neural network then further processes each output encoding individually. These output encodings are finally passed to the next encoder as its input, as well as the decoders.
2020c
- (Wikipedia, 2020) ⇒ https://en.wikipedia.org/wiki/Transformer_(machine_learning_model)#Decoder Retrieved:2020-9-15.
- Each decoder consists of three major components: a self-attention mechanism, an attention mechanism over the encodings, and a feed-forward neural network. The decoder functions in a similar fashion to the encoder, but an additional attention mechanism is inserted which instead draws relevant information from the encodings generated by the encoders.
Like the first encoder, the first decoder takes positional information and embeddings of the output sequence as its input, rather than encodings. Since the transformer should not use the current or future output to predict an output though, the output sequence must be partially masked to prevent this reverse information flow. The last decoder is followed by a final linear transformation and softmax layer, to produce the output probabilities over the vocabulary.
- Each decoder consists of three major components: a self-attention mechanism, an attention mechanism over the encodings, and a feed-forward neural network. The decoder functions in a similar fashion to the encoder, but an additional attention mechanism is inserted which instead draws relevant information from the encodings generated by the encoders.
2020d
- (Celikyilmaz et al., 2020) ⇒ Asli Celikyilmaz, Elizabeth Clark, and Jianfeng Gao. (2020). “Evaluation of Text Generation: A Survey.” In: arXiv preprint arXiv:2006.14799.
2019
- (Zhang, Goodfellow et al., 2019) ⇒ Han Zhang, Ian Goodfellow, Dimitris Metaxas, and Augustus Odena. (2019). “Self-attention Generative Adversarial Networks". In: International Conference on Machine Learning, pp. 7354-7363 . PMLR,
2018a
- (Alammar, 2018) ⇒ Jay Alammar (June 27, 2018). "The Illustrated Transformer". In: Alammar Blog.
- QUOTE: The first step in calculating self-attention is to create three vectors from each of the encoder’s input vectors (in this case, the embedding of each word). So for each word, we create a Query vector, a Key vector, and a Value vector. These vectors are created by multiplying the embedding by three matrices that we trained during the training process ...)
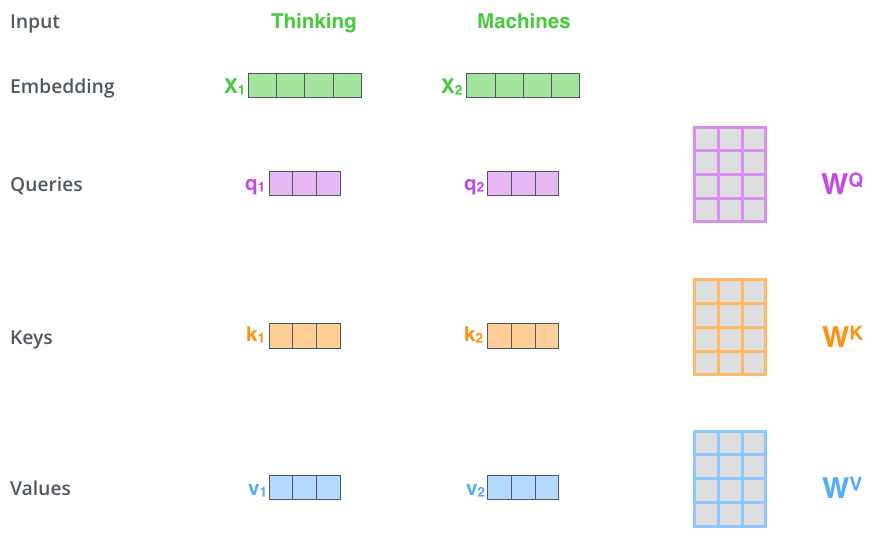
(...)
(...) to calculate the Query, Key, and Value matrices. We do that by packing our embeddings into a matrix $X$, and multiplying it by the weight matrices we’ve trained ($W^Q$, $W^K$, $W^V$).
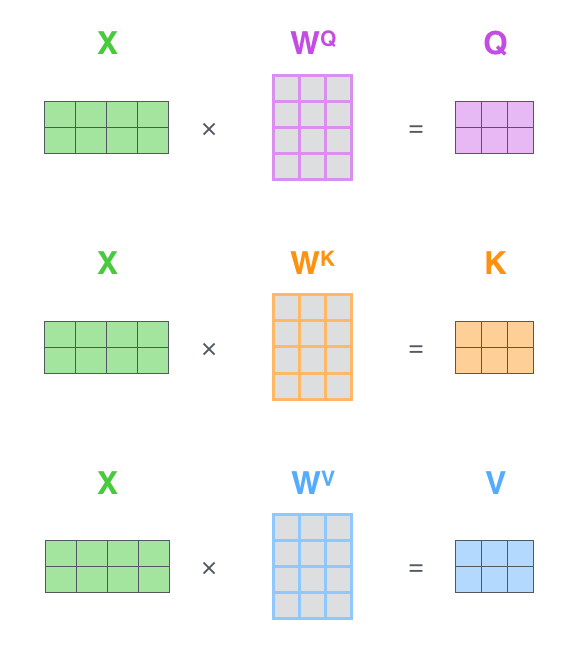
Every row in the $X$ matrix corresponds to a word in the input sentence. We again see the difference in size of the embedding vector (512, or 4 boxes in the figure), and the q/k/v vectors (64, or 3 boxes in the figure)
Finally, since we’re dealing with matrices, we can condense steps two through six in one formula to calculate the outputs of the self-attention layer.
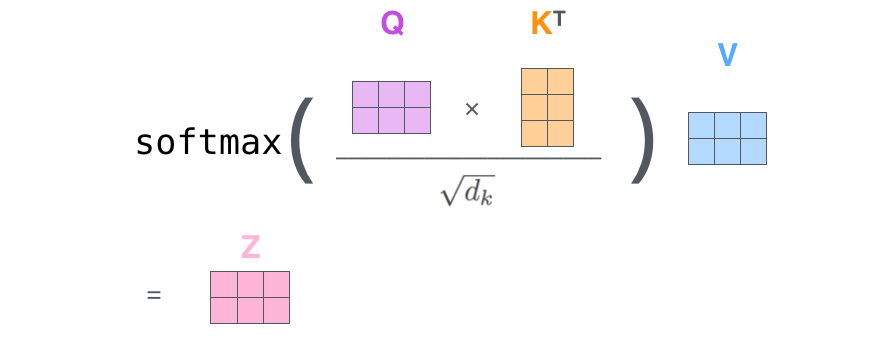
The self-attention calculation in matrix form
- QUOTE: The first step in calculating self-attention is to create three vectors from each of the encoder’s input vectors (in this case, the embedding of each word). So for each word, we create a Query vector, a Key vector, and a Value vector. These vectors are created by multiplying the embedding by three matrices that we trained during the training process ...)
2018b
- (Shaw et al., 2018) ⇒ Peter Shaw, Jakob Uszkoreit, and Ashish Vaswani. (2018). “Self-Attention with Relative Position Representations.” In: Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT 2018) Volume 2 (Short Papers).
- QUOTE: We also want to avoid broadcasting relative position representations. However, both issues can be resolved by splitting the computation of eq.(4) into two terms:
- QUOTE: We also want to avoid broadcasting relative position representations. However, both issues can be resolved by splitting the computation of eq.(4) into two terms:
|
$e_{i j}=\dfrac{x_{i} W^{Q}\left(x_{j} W^{K}\right)^{T}+x_{i} W^{Q}\left(a_{i j}^{K}\right)^{T}}{\sqrt{d_{z}}}$ |
(5) |
- The first term is identical to eq.(2), and can be computed as described above. For the second term involving relative position representations, tensor reshaping can be used to compute $n$ parallel multiplications of $bh\times d_z$ and $d_z\times n$ matrices. Each matrix multiplication computes contributions to $e_{ij}$ for all heads and batches, corresponding to a particular sequence position. Further reshaping allows adding the two terms. The same approach can be used to efficiently compute eq.(3).
2017a
- (Vaswani et al., 2017) ⇒ Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. (2017). “Attention is all You Need.” In: Advances in Neural Information Processing Systems.
- QUOTE: We call our particular attention “Scaled Dot-Product Attention” (Figure 2). The input consists of queries and keys of dimension [math]\displaystyle{ d_k }[/math], and values of dimension [math]\displaystyle{ d_v }[/math]. We compute the dot products of the query with all keys, divide each by [math]\displaystyle{ \sqrt{d_k} }[/math] , and apply a softmax function to obtain the weights on the values.
- QUOTE: We call our particular attention “Scaled Dot-Product Attention” (Figure 2). The input consists of queries and keys of dimension [math]\displaystyle{ d_k }[/math], and values of dimension [math]\displaystyle{ d_v }[/math]. We compute the dot products of the query with all keys, divide each by [math]\displaystyle{ \sqrt{d_k} }[/math] , and apply a softmax function to obtain the weights on the values.

|
- In practice, we compute the attention function on a set of queries simultaneously, packed together into a matrix [math]\displaystyle{ Q }[/math]. The keys and values are also packed together into matrices [math]\displaystyle{ K }[/math] and [math]\displaystyle{ V }[/math]. We compute the matrix of outputs as:
| [math]\displaystyle{ Attention(Q,K,V)=\mathrm{softmax}\left(\dfrac{QK_T}{\sqrt{d_k}}\right)V }[/math] | (1) |
2017b
- (Lin et al., 2017) ⇒ Zhouhan Lin, Minwei Feng, Cicero Nogueira dos Santos, Mo Yu, Bing Xiang, Bowen Zhou, and Yoshua Bengio. (2017). “A Structured Self-attentive Sentence Embedding.” In: Proceedings of the 5th International Conference on Learning Representations (ICRL-2017).
- QUOTE: Computing the linear combination requires the self-attention mechanism. The attention mechanism takes the whole LSTM hidden states $H$ as input, and outputs a vector of weights $a$:
|
$\mathbf{a} = softmax\left(\mathbf{w_{s2}}tanh\left(W_{s1}H^T\right)\right) $ |
(5) |
- Here $W_{s1}$ is a weight matrix with a shape of $d_a$-by-$2u$. and $\mathbf{w_{s2}}$ is a vector of parameters with size $d_a$, where $d_a$ is a hyperparameter we can set arbitrarily. Since $H$ is sized $n$-by-$2u$, the annotation vector a will have a size $n$. the $softmax(\cdot)$ ensures all the computed weights sum up to 1. Then we sum up the LSTM hidden states $H$ according to the weight provided by a to get a vector representation $m$ of the input sentence.
