Word Embedding System
A Word Embedding System is a text item embedding system that maps words into a vector representation.
- AKA: Word Representation Learning System, Word Modelling System, Word Vector Generation System, Text Representation System, Word Vector Space Modeling System.
- Context:
- It Implements a Word Embedding Algorithm to solve a Word Embedding Task.
- It can solve a Word Embedding Task by implementing a Word Embedding Algorithm.
- It is (usually) based on a Language Modeling System and a Feature Learning System.
- It can used to generate Word Embedding Dataset.
- It requires Word Embedding Model (WEM).
- It can be based on Sequence Tagging System.
- It can be based on a Bag-of-Words Mapping System or a Skip-Gram Mapping System.
- It can range from being a Sparse Word Embedding System to being a Dense Word Embedding System,
- It can range from being an In-Vocabulary (IV) Embedding System to being an Out-Of-Vocabulary (OOV) Embedding System.
- It can range from being Distributional Word Embedding Modeling System, to being a Deep Contextualized Word Representation System.
- It can range from being Contextual Word Embedding System, to being a Sentiment-Specific Word Embedding System, to being a Relevance-based Word Embedding System.
- It can range a Heuristic Word Vector Space Model Creation System to being a Data-Driven Word Vector Space Model Creation System.
- It can range from being a Continuous Bag-of-Words Embedding System to being a Continuous Skip-Gram Word Embedding System.
- Example(s):
- BERT Embedding System (Devlin et al., 2019),
- DISSECT System (Dinu et al., 2013),
- ELMo System (Peters et al., 2018),
- fastText System (Bojanowski et al., 2017),
- GenSim System (Rehurek & Sojka, 2010),
- GloVe System (Pennington et al., 2014),
- Indra System (Sales et al., 2018),
- MIMICK System (Pinter et al., 2017),
- Polyglot System (Al-Rfou et al., 2013),
- SENNA Embedding System (Collobert & Weston, 2008),
- SumEmbed System (Botha & Blunsom, 2014),
- VarEmbed System (Bhatia et al., 2016),
- Word2Vec System (Mikolov et al., 2014).
https://remykarem.github.io/word2vec-demo/- …
- Counter-Example(s):
- See: One-Hot Encoding System, DeepLearning4J, Word Similarity Task, Word Analogy Task, Distributional Co-Occurrence Word Vector, Term Vector Space, Sentiment Analysis, Natural Language Processing, Language Model, Sequence Tagging, Vector (Mathematics), Real Numbers, Embedding, Vector Space, Neural Net Language Model, Dimensionality Reduction, co-Occurrence Matrix, Syntactic Parsing, S-Space Package.
References
2021a
- (Wikipedia, 2021) ⇒ https://en.wikipedia.org/wiki/Word_embedding Retrieved:2021-4-18.
- In natural language processing (NLP), Word embedding is a term used for the representation of words for text analysis, typically in the form of a real-valued vector that encodes the meaning of the word such that the words that are closer in the vector space are expected to be similar in meaning. Word embeddings can be obtained using a set of language modeling and feature learning techniques where words or phrases from the vocabulary are mapped to vectors of real numbers. Conceptually it involves a mathematical embedding from a space with many dimensions per word to a continuous vector space with a much lower dimension. Methods to generate this mapping include neural networks, dimensionality reduction on the word co-occurrence matrix, probabilistic models, explainable knowledge base method, and explicit representation in terms of the context in which words appear. Word and phrase embeddings, when used as the underlying input representation, have been shown to boost the performance in NLP tasks such as syntactic parsing and sentiment analysis.
2021b
- (TensorFlow Tutorials, 2021) ⇒ https://www.tensorflow.org/tutorials/text/word_embeddings Retrieved: 2021-05-09.
- QUOTE: Word embeddings give us a way to use an efficient, dense representation in which similar words have a similar encoding. Importantly, you do not have to specify this encoding by hand. An embedding is a dense vector of floating point values (the length of the vector is a parameter you specify). Instead of specifying the values for the embedding manually, they are trainable parameters (weights learned by the model during training, in the same way a model learns weights for a dense layer). It is common to see word embeddings that are 8-dimensional (for small datasets), up to 1024-dimensions when working with large datasets. A higher dimensional embedding can capture fine-grained relationships between words, but takes more data to learn.
2020
- (Jurafsky & Martin, 2020) ⇒ Daniel Jurafsky, and James H. Martin. (2020). “Vector Semantics and Embeddings.” In: Speech and Language Processing (3rd ed. draft).
- QUOTE: In vector semantics, a word is modeled as a vector — a point in high-dimensional space, also called an embedding (...)
- Vector semantic models fall into two classes: sparse and dense. In sparse models each dimension corresponds to a word in the vocabulary $V$ and cells are functions of co-occurrence counts. The term-document matrix has a row for each word (term) in the vocabulary and a column for each document. The word-context or term-term matrix has a row for each (target) word in the vocabulary and a column for each context term in the vocabulary. Two sparse weightings are common: the tf-idf weighting which weights each cell by its term frequency and inverse document frequency, and PPMI (pointwise positive mutual information) most common for word-context matrices.
- QUOTE: In vector semantics, a word is modeled as a vector — a point in high-dimensional space, also called an embedding (...)
2017a
- (Bojanowski et al., 2017) ⇒ Piotr Bojanowski, Edouard Grave, Armand Joulin, and Tomas Mikolov. (2017). “Enriching Word Vectors with Subword Information.” In: Transactions of the Association for Computational Linguistics, 5.
- QUOTE: Learning continuous representations of words has a long history in natural language processing (Rumelhart et al., 1988). These representations are typically derived from large unlabeled corpora using co-occurrence statistics (Deerwester et al., 1990; Schütze, 1992; Lund and Burgess, 1996). A large body of work, known as distributional semantics, has studied the properties of these methods (Turneyet al., 2010; Baroni and Lenci, 2010). In the neural network community, Collobert and Weston (2008) proposed to learn word embeddings using a feedforward neural network, by predicting a word based on the two words on the left and two words on the right. More recently, Mikolov et al. (2013b) proposed simple log-bilinear models to learn continuous representations of words on very large corpora efficiently.
2017b
- (Dhingra et al., 2017) ⇒ Bhuwan Dhingra, Hanxiao Liu, Ruslan Salakhutdinov, and William W. Cohen. (2017). “A Comparative Study of Word Embeddings for Reading Comprehension.” In: arXiv, abs/1703.00993.
- QUOTE: The two most popular methods for inducing word embeddings from text corpora are GloVe (Pennington et al., 2014) and word2vec (Mikolov et al., 2013). These packages also provide off-the-shelf (OTS) embeddings trained on large corpora[1]. While the GloVe package provides embeddings with varying sizes (50-300), word2vec only provides embeddings of size 300.
- ↑ The word2vec package contains embeddings for both capitalized and lowercase words. We convert all words to lowercase, and if a word has both lowercase and uppercase embeddings we use the lowercase version.
2017c
- (Pinter et al., 2017) ⇒ Yuval Pinter, Robert Guthrie, and Jacob Eisenstein. (2017). “Mimicking Word Embeddings Using Subword RNNs.” In: Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing (EMNLP 2017).
- QUOTE: One of the key advantages of word embeddings for natural language processing is that they enable generalization to words that are unseen in labeled training data, by embedding lexical features from large unlabeled datasets into a relatively low-dimensional Euclidean space. These low-dimensional embeddings are typically trained to capture distributional similarity, so that information can be shared among words that tend to appear in similar contexts. .
2016
- (Colyer, 2016) ⇒ Adrian Colyer (2016). “The Amazing Power of Word Vectors". In: The Morning Paper.
- QUOTE: At one level, it’s simply a vector of weights. In a simple 1-of-N (or ‘one-hot’) encoding every element in the vector is associated with a word in the vocabulary. The encoding of a given word is simply the vector in which the corresponding element is set to one, and all other elements are zero.
Suppose our vocabulary has only five words:
King,Queen,Man,Woman, andChild. We could encode the word ‘Queen’ as:
- QUOTE: At one level, it’s simply a vector of weights. In a simple 1-of-N (or ‘one-hot’) encoding every element in the vector is associated with a word in the vocabulary. The encoding of a given word is simply the vector in which the corresponding element is set to one, and all other elements are zero.
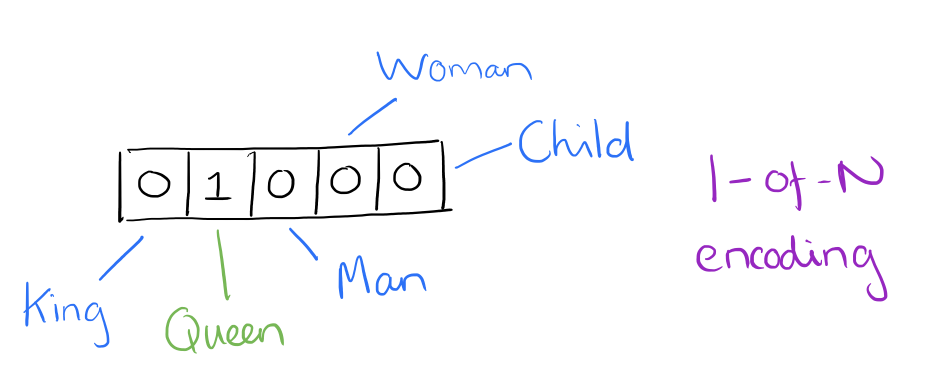
- Using such an encoding, there’s no meaningful comparison we can make between word vectors other than equality testing.
In word2vec, a distributed representation of a word is used. Take a vector with several hundred dimensions (say 1000). Each word is representated by a distribution of weights across those elements. So instead of a one-to-one mapping between an element in the vector and a word, the representation of a word is spread across all of the elements in the vector, and each element in the vector contributes to the definition of many words.
If I label the dimensions in a hypothetical word vector (there are no such pre-assigned labels in the algorithm of course), it might look a bit like this:
- Using such an encoding, there’s no meaningful comparison we can make between word vectors other than equality testing.
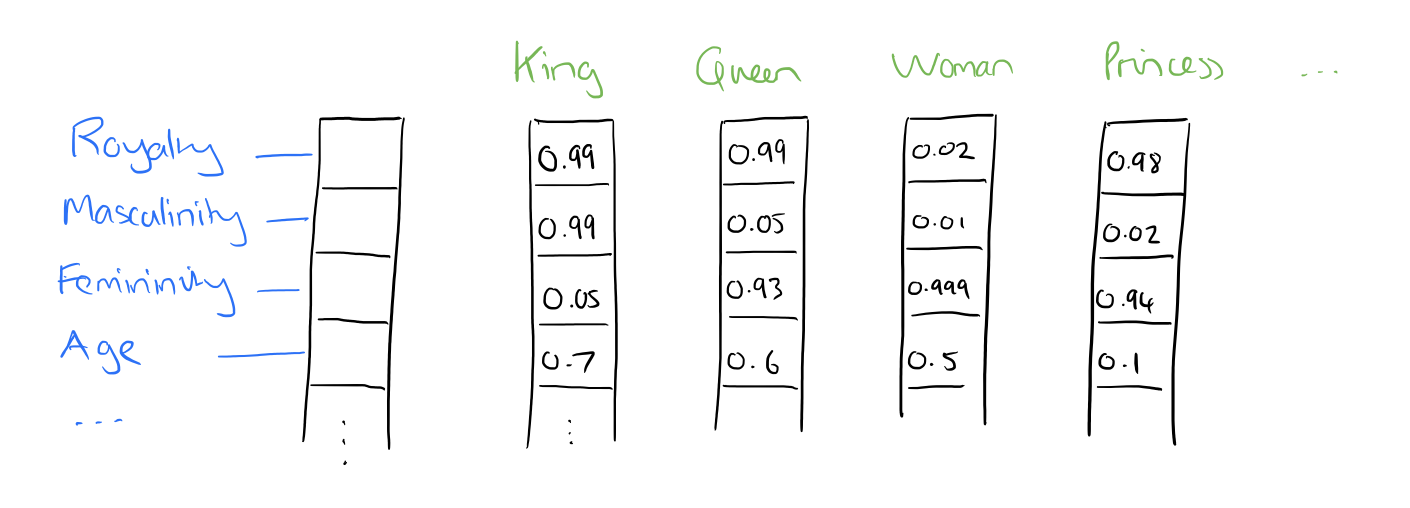
:: Such a vector comes to represent in some abstract way the ‘meaning’ of a word. And as we’ll see next, simply by examining a large corpus it’s possible to learn word vectors that are able to capture the relationships between words in a surprisingly expressive way. We can also use the vectors as inputs to a neural network.
2014a
- (Pennington et al., 2014) ⇒ Jeffrey Pennington, Richard Socher, and Christopher D. Manning. (2014). “GloVe: Global Vectors for Word Representation.” In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP 2014).
2014b
- (Mikolov et al., 2014) ⇒ Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. (2014). “Distributed Representations of Words and Phrases and their Compositionality.” In: Advances in Neural Information Processing Systems 26 (NIPS 2013).
2013a
- (Al-Rfou et al., 2013) ⇒ Rami Al-Rfou, Bryan Perozzi, and Steven Skiena (2013). "Polyglot: Distributed word representations for multilingual NLP". In: Proceedings of the Conference on Natural Language Learning (CoNLL 2013).
- QUOTE: Distributed word representations (word embeddings) map the index of a word in a dictionary to a feature vector in high-dimension space. Every dimension contributes to multiple concepts, and every concept is expressed by a combination of subset of dimensions. Such mapping is learned by back-propagating the error of a task through the model to update random initialized embeddings. The task is usually chosen such that examples can be automatically generated from unlabeled data (i.e so it is unsupervised). In case of language modeling, the task is to predict the last word of a phrase that consists of n words.
2013b
- (Mikolov et al., 2014) ⇒ Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. (2014). “Distributed Representations of Words and Phrases and their Compositionality.” In: Advances in Neural Information Processing Systems 26 (NIPS 2013).
2008
- (Collobert & Weston, 2008) ⇒ R. Collobert and J. Weston (2008). "A Unified Architecture For Natural Language Processing: Deep Neural Networks With Multitask Learning". In: Proceedings of the Twenty-Fifth International Conference on Machine Learning (ICML 2008).