Neural Network Weight Size
A Neural Network Weight Size is a number of Artificial Neural Connections between Neural Network Layers.
- AKA: Artificial Neural Network Weight Size, NN Weight Size, ANN Weight Size.
- Context:
- It is defined as the number of artificial neurons in a Neural Network Layer ([math]\displaystyle{ n_i }[/math]) multiplied by the number of of artificial neuron in adjacent layer ([math]\displaystyle{ n_{i+1} }[/math]), i.e.
[math]\displaystyle{ S_{i}=n_i\times n_{i+1}\quad }[/math] with [math]\displaystyle{ \quad i=1,\cdots, M-1. }[/math]
where [math]\displaystyle{ M }[/math] the total number of Neural Network Layers.
- It is defined as the number of artificial neurons in a Neural Network Layer ([math]\displaystyle{ n_i }[/math]) multiplied by the number of of artificial neuron in adjacent layer ([math]\displaystyle{ n_{i+1} }[/math]), i.e.
- Example(s):
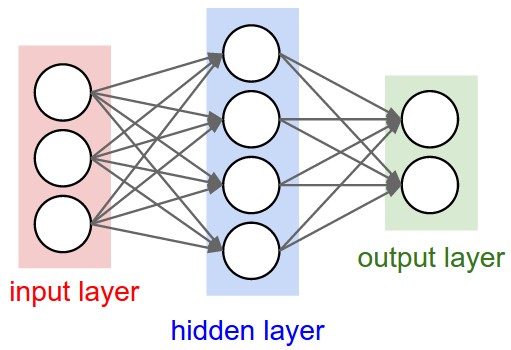
- A 2-Layer Neural Network such as
has [math]\displaystyle{ S_1 =3 \times 4 = 12 }[/math] and [math]\displaystyle{ S_2=4 \times 2 = 8 }[/math]. The total NN Weight Size (i.e. number of connections) is 20.
- A 3-Layer Neural Network such as
has [math]\displaystyle{ S_1 =3 \times 4 = 12 }[/math], [math]\displaystyle{ S_2=4 \times 5 = 20 }[/math] and [math]\displaystyle{ S_3=5 \times 2 = 10 }[/math]. The total NN Weight Size (i.e. number of connections) is 42.
- …
- A 2-Layer Neural Network such as
- Counter-Example(s):
- See: Neuron Activation Function, Neural Network Weight Matrix, Neural Network Transfer Function, Neural Network Topology.
References
2017
- (CS231n, 2017) ⇒ http://cs231n.github.io/neural-networks-1/#layers Retrieved: 2017-12-31
- Neural Networks as neurons in graphs. Neural Networks are modeled as collections of neurons that are connected in an acyclic graph. In other words, the outputs of some neurons can become inputs to other neurons. Cycles are not allowed since that would imply an infinite loop in the forward pass of a network. Instead of an amorphous blobs of connected neurons, Neural Network models are often organized into distinct layers of neurons. For regular neural networks, the most common layer type is the fully-connected layer in which neurons between two adjacent layers are fully pairwise connected, but neurons within a single layer share no connections. Below are two example Neural Network topologies that use a stack of fully-connected layers:

|
|
Left: A 2-layer Neural Network (one hidden layer of 4 neurons (or units) and one output layer with 2 neurons), and three inputs. Right:A 3-layer neural network with three inputs, two hidden layers of 4 neurons each and one output layer. Notice that in both cases there are connections (synapses) between neurons across layers, but not within a layer. |
- Naming conventions. Notice that when we say N-layer neural network, we do not count the input layer. Therefore, a single-layer neural network describes a network with no hidden layers (input directly mapped to output). In that sense, you can sometimes hear people say that logistic regression or SVMs are simply a special case of single-layer Neural Networks. You may also hear these networks interchangeably referred to as “Artificial Neural Networks” (ANN) or “Multi-Layer Perceptrons” (MLP). Many people do not like the analogies between Neural Networks and real brains and prefer to refer to neurons as units.
Output layer. Unlike all layers in a Neural Network, the output layer neurons most commonly do not have an activation function (or you can think of them as having a linear identity activation function). This is because the last output layer is usually taken to represent the class scores (e.g. in classification), which are arbitrary real-valued numbers, or some kind of real-valued target (e.g. in regression).
Sizing neural networks. The two metrics that people commonly use to measure the size of neural networks are the number of neurons, or more commonly the number of parameters. Working with the two example networks in the above picture:
::* The first network (left) has [math]\displaystyle{ 4 + 2 = 6 }[/math] neurons (not counting the inputs), [math]\displaystyle{ [3 \times 4] + [4 \times 2] = 20 }[/math] weights and 4 + 2 = 6 biases, for a total of 26 learnable parameters.
- The second network (right) has [math]\displaystyle{ 4 + 4 + 1 = 9 }[/math] neurons, [math]\displaystyle{ [3 \times 4] + [4 \times 4] + [4 \times 1] = 12 + 16 + 4 = 32 }[/math] weights and [math]\displaystyle{ 4 + 4 + 1 = 9 }[/math] biases, for a total of 41 learnable parameters.
To give you some context, modern Convolutional Networks contain on orders of 100 million parameters and are usually made up of approximately 10-20 layers (hence deep learning).
- The second network (right) has [math]\displaystyle{ 4 + 4 + 1 = 9 }[/math] neurons, [math]\displaystyle{ [3 \times 4] + [4 \times 4] + [4 \times 1] = 12 + 16 + 4 = 32 }[/math] weights and [math]\displaystyle{ 4 + 4 + 1 = 9 }[/math] biases, for a total of 41 learnable parameters.
- Naming conventions. Notice that when we say N-layer neural network, we do not count the input layer. Therefore, a single-layer neural network describes a network with no hidden layers (input directly mapped to output). In that sense, you can sometimes hear people say that logistic regression or SVMs are simply a special case of single-layer Neural Networks. You may also hear these networks interchangeably referred to as “Artificial Neural Networks” (ANN) or “Multi-Layer Perceptrons” (MLP). Many people do not like the analogies between Neural Networks and real brains and prefer to refer to neurons as units.
1998
- (Wilson,1998) ⇒ Bill Wilson, (1998 - 2012). "Weight"] in "The Machine Learning Dictionary".
- QUOTE: Take above DNN architecture, for example, there are 3 groups of weights from the input layer to first hidden layer, first to second hidden layer and second hidden layer to output layer. Bias unit links to every hidden node and which affects the output scores, but without interacting with the actual data. In our R implementation, we represent weights and bias by the matrix. Weight size is defined by,
(number of neurons layer M) X (number of neurons in layer M+1)
and weights are initialized by random number from rnorm. Bias is just a one dimensional matrix with the same size of neurons and set to zero.

