2021 ScalingScalingLawswithBoardGame

• (Jones, 2021) ⇒ Andy L. Jones. (2021). “Scaling Scaling Laws with Board Games.” doi:10.48550/arXiv.2104.03113

Subject Headings: LLM Scaling Laws.

Notes

1. Introduction to Scaling Laws in Reinforcement Learning: Offers a lucid explanation of how scaling laws (originally prominent in NLP and vision) can apply to RL settings. This approach demonstrates the potential for scaling laws to unify multiple aspects of training, including the size of the model, the data, and even the complexity of the environment. The authors highlight how smaller-scale experiments can reliably inform predictions about more expensive or larger-scale tasks.
2. Compute-Performance Trade-Off Frontiers: Provides an in-depth look at how training compute correlates with skill (as measured by Elo) across different board sizes and model architectures. These frontiers clearly illustrate how even minor increases in compute can yield large performance gains, helping researchers target the most efficient spending of resources. The paper’s analysis also helps clarify why performance curves often follow a sigmoidal shape in AlphaZero-like RL systems.
3. Multi-Agent Evaluation and Elo Rating Methods: Demonstrates how to assess an agent’s skill in two-player, zero-sum games by matching different versions of trained agents against one another. The authors emphasize the importance of transitivity and discuss how to mitigate or detect non-transitive loop issues that can arise in multi-agent interactions. Their approach using pairwise matchups and reference points (e.g., a perfect play engine) is a robust method to obtain accurate Elo ratings.
4. Hex Environment and Problem Scaling: Uses the strategic board game Hex (with adjustable board size) as a test bed to show that the performance laws identified on small boards generalize well to larger boards. This scaling of the problem itself—rather than only the model—reveals a deeper insight into how difficulty exponentially increases. It also showcases why simpler rule sets (compared to Go or Chess) are beneficial for reproducible and efficient experimentation.
5. Advancing Monte Carlo Tree Search (MCTS) in Reinforcement Learning: Highlights a GPU-based regularized MCTS that can efficiently explore large batches of games, significantly speeding up training. The authors share useful design choices—such as reduced coefficients of exploration and specialized optimization steps—to stabilize and accelerate search-based RL. These refinements show that a careful balance of exploration and exploitation is key to extracting the most from limited compute.

1. Smooth Scaling Behavior Across Board Sizes: Finds that performance changes smoothly and predictably as board size increases, supporting the idea of consistent power-law or sigmoid-like curves in RL. This absence of abrupt performance “jumps” or “spikes” indicates that no hidden threshold or discrete insight is required to master larger boards. In turn, it suggests that scaling laws can bridge small and large tasks without discontinuous leaps in complexity or skill.
2. Practical Guidelines for Small vs. Large RL Experiments: Offers methodological examples and computational strategies for scaling up an experiment from a simple, low-resource environment to a much more demanding one. By demonstrating how data from smaller boards can anticipate results on bigger boards, the paper provides a roadmap for researchers facing limited budgets. These guidelines also empower them to iterate faster and focus on the most promising settings before undertaking computationally expensive runs.
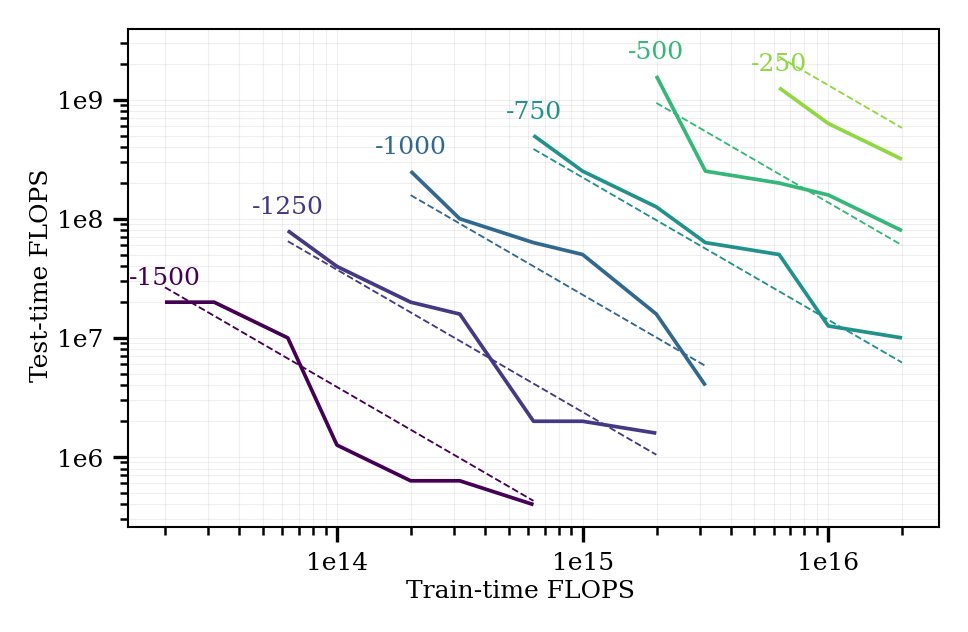
3. Train-Time vs. Test-Time Compute Trade-Off: Reveals that investing more compute during the training phase can reduce the inference-phase budget significantly, while maintaining or improving performance. This linear relationship in log-compute offers a novel angle for optimizing the total cost of deployment, whether in industrial or research applications. It underscores how one can strategically decide whether to spend resources “up front” while training or “on the fly” during real-time inference.
4. Methodological Rigor in Large-Scale Evaluations: Details how to efficiently structure and evaluate thousands (or millions) of multi-agent matchups, each requiring substantial GPU-based simulations. Their system of parallelization and snapshot-based comparisons ensures stable skill estimates and reliable performance curves across many runs. This rigorous approach can serve as a template for any domain needing robust comparisons among large numbers of agents or policies.
5. Implications for Future Research on Scaling in Reinforcement Learning: Discusses the broader significance of these results, hinting that problem scaling plus model scaling may generalize well beyond Hex to more complex multi-agent domains. If the phenomenon proves to be as universal as in language or vision tasks, it could enable small-scale RL work to profoundly impact large-scale game or simulation challenges. Moreover, the consistent success in forecasting performance opens up a wealth of possibilities for resource-limited labs to contribute to fundamental scaling research.

Cited By

• http://scholar.google.com/scholar?q=%222021%22+Scaling+Scaling+Laws+with+Board+Games

Quotes

Abstract

The largest experiments in machine learning now require resources far beyond the budget of all but a few institutions. Fortunately, it has recently been shown that the results of these huge experiments can often be extrapolated from the results of a sequence of far smaller, cheaper experiments. In this work, we show that not only can the extrapolation be done based on the size of the model, but on the size of the problem as well. By conducting a sequence of experiments using AlphaZero and Hex, we show that the performance achievable with a fixed amount of compute degrades predictably as the game gets larger and harder. Along with our main result, we further show that the test-time and train-time compute available to an agent can be traded off while maintaining performance.

References

;

	Author	volume	Date Value	title	type	journal	titleUrl	doi	note	year
2021 ScalingScalingLawswithBoardGame	Andy L. Jones			Scaling Scaling Laws with Board Games				10.48550/arXiv.2104.03113		2021