Power Law Distribution Function Family
A Power Law Distribution Function Family is a probability density function that is a Power Law function.
- Context:
- It can (typically) describe a relationship between two quantities where one is a constant power of the other.
- It can (typically) exhibit heavy tails and a shrinking proportion of larger values compared to smaller values.
- It can (often) be observed in real-world phenomena such as city populations, earthquake magnitudes, and internet connectivity.
- It can (often) be used to model distributions in Economics, Biology, and Physics.
- It can be related to phenomena like the Pareto Principle and Zipf's Law.
- ...
- Example(s):
- The distribution of income in an economy, often modeled by a Pareto distribution.
- The frequency of words in a language, following Zipf's law.
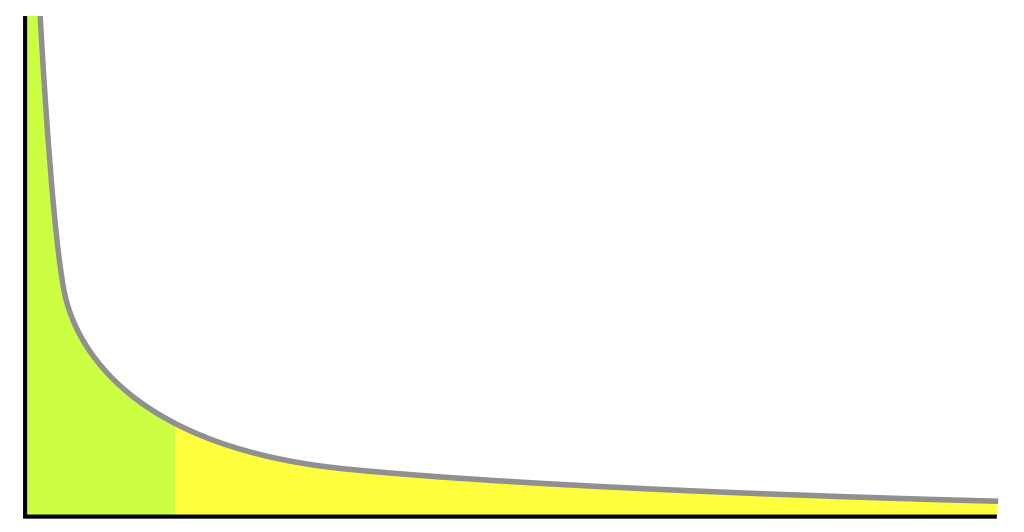
- Pareto Distribution.
- ...
- Counter-Example(s):
- See: Power Law Probability Distribution, Power Law Function, Exponentiation, Statistics, Function (Mathematics), Relative Change And Difference.
References
2024
- (Wikipedia, 2024) ⇒ https://en.wikipedia.org/wiki/Power_law Retrieved:2024-2-6.
- In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a relative change in the other quantity proportional to a power of the change, independent of the initial size of those quantities: one quantity varies as a power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four. The rate of change exhibited in these relationships is said to be multiplicative.

2015
- (Wikipedia, 2015) ⇒ http://en.wikipedia.org/wiki/Power_law Retrieved:2015-3-19.
- In statistics, a power law is a functional relationship between two quantities, where one quantity varies as a power of another. For instance, the number of cities having a certain population size is found to vary as a power of the size of the population. Empirical power-law distributions hold only approximately or over a limited range.
2015
- (Wikipedia, 2015) ⇒ http://en.wikipedia.org/wiki/Power_law#Power-law_probability_distributions Retrieved:2015-3-19.
- In a looser sense, a power-law probability distribution is a distribution whose density function (or mass function in the discrete case) has the form : [math]\displaystyle{ p(x) \propto L(x) x^{-\alpha} }[/math] where [math]\displaystyle{ \alpha \gt 1 }[/math] , and [math]\displaystyle{ L(x) }[/math] is a slowly varying function, which is any function that satisfies [math]\displaystyle{ \lim_{x\rightarrow\infty} L(t\,x) / L(x) = 1 }[/math] with [math]\displaystyle{ t }[/math] constant and [math]\displaystyle{ t \gt 0 }[/math] . This property of [math]\displaystyle{ L(x) }[/math] follows directly from the requirement that [math]\displaystyle{ p(x) }[/math] be asymptotically scale invariant; thus, the form of [math]\displaystyle{ L(x) }[/math] only controls the shape and finite extent of the lower tail. For instance, if [math]\displaystyle{ L(x) }[/math] is the constant function, then we have a power law that holds for all values of [math]\displaystyle{ x }[/math] . In many cases, it is convenient to assume a lower bound [math]\displaystyle{ x_{\mathrm{min}} }[/math] from which the law holds. Combining these two cases, and where [math]\displaystyle{ x }[/math] is a continuous variable, the power law has the form : [math]\displaystyle{ p(x) = \frac{\alpha-1}{x_\min} \left(\frac{x}{x_\min}\right)^{-\alpha}, }[/math] where the pre-factor to [math]\displaystyle{ \frac{\alpha-1}{x_\min} }[/math] is the normalizing constant. We can now consider several properties of this distribution. For instance, its moments are given by : [math]\displaystyle{ \langle x^{m} \rangle = \int_{x_\min}^\infty x^{m} p(x) \,\mathrm{d}x = \frac{\alpha-1}{\alpha-1-m}x_\min^m }[/math] which is only well defined for [math]\displaystyle{ m \lt \alpha -1 }[/math]. That is, all moments [math]\displaystyle{ m \geq \alpha - 1 }[/math] diverge: when [math]\displaystyle{ \alpha\lt 2 }[/math], the average and all higher-order moments are infinite; when [math]\displaystyle{ 2\lt \alpha\lt 3 }[/math], the mean exists, but the variance and higher-order moments are infinite, etc. For finite-size samples drawn from such distribution, this behavior implies that the central moment estimators (like the mean and the variance) for diverging moments will never converge – as more data is accumulated, they continue to grow. These power-law probability distributions are also called Pareto-type distributions, distributions with Pareto tails, or distributions with regularly varying tails.
Another kind of power-law distribution, which does not satisfy the general form above, is the power law with an exponential cutoff: [math]\displaystyle{ p(x) \propto L(x) x^{-\alpha} \mathrm{e}^{-\lambda x}. }[/math] In this distribution, the exponential decay term [math]\displaystyle{ \mathrm{e}^{-\lambda x} }[/math] eventually overwhelms the power-law behavior at very large values of [math]\displaystyle{ x }[/math] . This distribution does not scale and is thus not asymptotically a power law; however, it does approximately scale over a finite region before the cutoff. (Note that the pure form above is a subset of this family, with [math]\displaystyle{ \lambda=0 }[/math] .) This distribution is a common alternative to the asymptotic power-law distribution because it naturally captures finite-size effects. For instance, although the Gutenberg–Richter law is commonly cited as an example of a power-law distribution, the distribution of earthquake magnitudes cannot scale as a power law in the limit [math]\displaystyle{ x\rightarrow\infty }[/math] because there is a finite amount of energy in the Earth's crust and thus there must be some maximum size to an earthquake. As the scaling behavior approaches this size, it must taper off.
The Tweedie distributions are a family of statistical models characterized by closure under additive and reproductive convolution as well as under scale transformation. Consequently these models all express a power-law relationship between the variance and the mean. These models have a fundamental role as foci of mathematical convergence similar to the role that the normal distribution has as a focus in the central limit theorem. This convergence effect explains why the variance-to-mean power law manifests so widely in natural processes, as with Taylor's law in ecology and with fluctuation scaling[1] in physics. It can also be shown that this variance-to-mean power law, when demonstrated by the method of expanding bins, implies the presence of 1/f noise and that 1/f noise can arise as a consequence of this Tweedie convergence effect.[2]
- In a looser sense, a power-law probability distribution is a distribution whose density function (or mass function in the discrete case) has the form : [math]\displaystyle{ p(x) \propto L(x) x^{-\alpha} }[/math] where [math]\displaystyle{ \alpha \gt 1 }[/math] , and [math]\displaystyle{ L(x) }[/math] is a slowly varying function, which is any function that satisfies [math]\displaystyle{ \lim_{x\rightarrow\infty} L(t\,x) / L(x) = 1 }[/math] with [math]\displaystyle{ t }[/math] constant and [math]\displaystyle{ t \gt 0 }[/math] . This property of [math]\displaystyle{ L(x) }[/math] follows directly from the requirement that [math]\displaystyle{ p(x) }[/math] be asymptotically scale invariant; thus, the form of [math]\displaystyle{ L(x) }[/math] only controls the shape and finite extent of the lower tail. For instance, if [math]\displaystyle{ L(x) }[/math] is the constant function, then we have a power law that holds for all values of [math]\displaystyle{ x }[/math] . In many cases, it is convenient to assume a lower bound [math]\displaystyle{ x_{\mathrm{min}} }[/math] from which the law holds. Combining these two cases, and where [math]\displaystyle{ x }[/math] is a continuous variable, the power law has the form : [math]\displaystyle{ p(x) = \frac{\alpha-1}{x_\min} \left(\frac{x}{x_\min}\right)^{-\alpha}, }[/math] where the pre-factor to [math]\displaystyle{ \frac{\alpha-1}{x_\min} }[/math] is the normalizing constant. We can now consider several properties of this distribution. For instance, its moments are given by : [math]\displaystyle{ \langle x^{m} \rangle = \int_{x_\min}^\infty x^{m} p(x) \,\mathrm{d}x = \frac{\alpha-1}{\alpha-1-m}x_\min^m }[/math] which is only well defined for [math]\displaystyle{ m \lt \alpha -1 }[/math]. That is, all moments [math]\displaystyle{ m \geq \alpha - 1 }[/math] diverge: when [math]\displaystyle{ \alpha\lt 2 }[/math], the average and all higher-order moments are infinite; when [math]\displaystyle{ 2\lt \alpha\lt 3 }[/math], the mean exists, but the variance and higher-order moments are infinite, etc. For finite-size samples drawn from such distribution, this behavior implies that the central moment estimators (like the mean and the variance) for diverging moments will never converge – as more data is accumulated, they continue to grow. These power-law probability distributions are also called Pareto-type distributions, distributions with Pareto tails, or distributions with regularly varying tails.