Maximum Common Subgraph
(Redirected from maximum common subgraph)
Jump to navigation
Jump to search
A Maximum Common Subgraph (MCS) is a graph that is subgraph of two graphs and that has many vertices as possible.
- Context:
- It can be calculated using a Maximum Common Subgraph Algorithm.
- It can range from being a Connected Maximum Common Subgraph (cMCS) to being a Disconnected Maximum Common Subgraph (dMCS).
- Example(s):
- Counter-Example(s):
- See: Maximum Common Subgraph System, Maximum Common Subgraph Task, Graph Theory, Graph Edge, Graph Node.
References
2018a
- (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Maximum_common_subgraph Retrieved:2018-11-20.
- In graph theory and theoretical computer science, a maximum common subgraph may mean either:
- Maximum common induced subgraph, a graph that is an induced subgraph of two given graphs and has as many vertices as possible.
- Maximum common edge subgraph, a graph that is a subgraph of two given graphs and has as many edges as possible.
- In graph theory and theoretical computer science, a maximum common subgraph may mean either:
2018b
- (Duesbury et al., 2018) ⇒ Edmund Duesbury, John Holliday, and Peter Willett. (2018). “Comparison of Maximum Common Subgraph Isomorphism Algorithms for the Alignment of 2D Chemical Structures.” In: ChemMedChem Journal, 13(6). doi:10.1002/cmdc.201700482, PMID: 29057611
- QUOTE: There are two distinct types of MCS. The connected MCS (hereafter cMCS) represents the largest single fragment (in terms of either the number of atoms or the number of bonds) common to two compounds when they are aligned; whereas the disconnected MCS (hereafter dMCS) can contain multiple fragments and is the set of fragments that maximises the number of atoms or bonds in the MCS. The connected and disconnected forms of the MCS are illustrated in Figure 1. There are two additional subdivisions of the MCS: the maximum common edge‐induced subgraph (MCES) representing all the edges (i.e., bonds) between two graphs; and the maximum common node‐induced subgraph (MCIS) representing the nodes (i.e., atoms) in common between two graphs with their respective end‐points preserved.
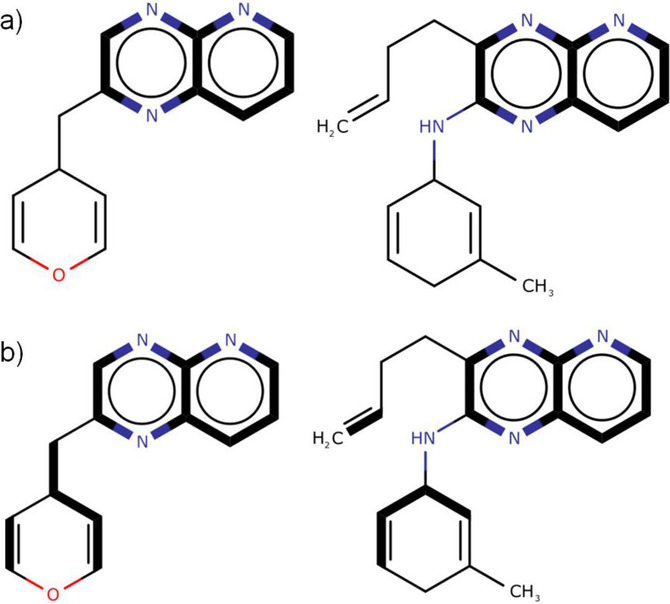
Figure 1. Types of MCES (the MCS in each pair of compounds represented by bold edges): a) cMCS between the two molecular graphs; b) dMCS between the same two molecular graphs.
- QUOTE: There are two distinct types of MCS. The connected MCS (hereafter cMCS) represents the largest single fragment (in terms of either the number of atoms or the number of bonds) common to two compounds when they are aligned; whereas the disconnected MCS (hereafter dMCS) can contain multiple fragments and is the set of fragments that maximises the number of atoms or bonds in the MCS. The connected and disconnected forms of the MCS are illustrated in Figure 1. There are two additional subdivisions of the MCS: the maximum common edge‐induced subgraph (MCES) representing all the edges (i.e., bonds) between two graphs; and the maximum common node‐induced subgraph (MCIS) representing the nodes (i.e., atoms) in common between two graphs with their respective end‐points preserved.
2007
- (Abu-Khzam et al., 2007) ⇒ Faisal N. Abu-Khzam, Nagiza F. Samatova, Mohamad A. Rizk, and Michael A. Langston. (2007). “The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover.” In: Proceedings of 2007 IEEE/ACS International Conference on Computer Systems and Applications. doi:10.1109/AICCSA.2007.370907
- QUOTE: Graph H is said to be common to graphs [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] if both [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] contain induced subgraphs isomorphic to [math]\displaystyle{ H }[/math]. Maximum Common Subgraph (MCS) is usually posed as the following decision problem.
- Inputs: A pair of graphs, [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math], and a positive integer [math]\displaystyle{ k }[/math].
- Question: Do [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] have a common subgraph of order [math]\displaystyle{ k }[/math] or more?
- MCS finds application in many domains. It has been used in bioinformatics 15, chemistry [9, 10], pattern recognition [3, 8], and a variety of other areas. Unfortunately, MCS is an exceedingly difficult problem, with several well-known NP-complete problems reducing to it. The maximum clique problem, for example, corresponds to the special case in which [math]\displaystyle{ |G_1| = |G_2| }[/math] and [math]\displaystyle{ G_1 }[/math] is complete.
2002a
- (Raymond & Willett, 2002) ⇒ John W. Raymond, and Peter Willett. (2002). “Maximum Common Subgraph Isomorphism Algorithms for the Matching of Chemical Structures.” In: Journal of Computer-Aided Molecular Design, 16. doi:https://doi.org/10.1023/A:1021271615909
- QUOTE: Two graphs are said to be isomorphic if there is a one-to-one correspondence between their vertices and an edge only exists between two vertices in one graph if an edge exists between the two corresponding vertices in the other graph. An induced subgraph is a set [math]\displaystyle{ S }[/math] of vertices of a graph [math]\displaystyle{ G }[/math] and those edges of [math]\displaystyle{ G }[/math] with both end-points in [math]\displaystyle{ S }[/math]. A graph [math]\displaystyle{ G_{12} }[/math] is a common induced subgraph of graphs [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] if [math]\displaystyle{ G_{12} }[/math] is isomorphic to induced subgraphs of [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math]. A maximum common induced subgraph (MCIS) consists of a graph [math]\displaystyle{ G_{12} }[/math] with the largest number of vertices meeting the aforementioned property. Related to the MCIS is the maximum common edge subgraph (MCES). An MCES is a subgraph consisting of the largest number of edges common to both [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math]. In this treatment, the term MCS will be used to denote both the MCIS and MCES problems. (...)
The MCS between two graphs can be classified further by distinguishing between the connected and disconnected case. A connected MCS is an MCS whereby each vertex is connected to every other vertex by at least one path in the graph (i.e., the MCS consists of a single subgraph). A disconnected MCS is comprised of two or more subgraph components.
- QUOTE: Two graphs are said to be isomorphic if there is a one-to-one correspondence between their vertices and an edge only exists between two vertices in one graph if an edge exists between the two corresponding vertices in the other graph. An induced subgraph is a set [math]\displaystyle{ S }[/math] of vertices of a graph [math]\displaystyle{ G }[/math] and those edges of [math]\displaystyle{ G }[/math] with both end-points in [math]\displaystyle{ S }[/math]. A graph [math]\displaystyle{ G_{12} }[/math] is a common induced subgraph of graphs [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] if [math]\displaystyle{ G_{12} }[/math] is isomorphic to induced subgraphs of [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math]. A maximum common induced subgraph (MCIS) consists of a graph [math]\displaystyle{ G_{12} }[/math] with the largest number of vertices meeting the aforementioned property. Related to the MCIS is the maximum common edge subgraph (MCES). An MCES is a subgraph consisting of the largest number of edges common to both [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math]. In this treatment, the term MCS will be used to denote both the MCIS and MCES problems. (...)
2002b
- (Bunke et al., 2002) ⇒ Horst Bunke, Pasquale Foggia, Corrado Guidobaldi, Carlo Sansone, and Mario Vento. (2002). “A Comparison of Algorithms for Maximum Common Subgraph on Randomly Connected Graphs.” In: Proceedings of the Joint IAPR International Workshop on Structural, Syntactic, and Statistical Pattern Recognition. ISBN:ISBN:3-540-44011-9 doi:https://doi.org/10.1007/3-540-70659-3_12
- QUOTE: A graph [math]\displaystyle{ g }[/math] is called a maximum common subgraph of two graphs, [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math], if there exists no other common subgraph of [math]\displaystyle{ g_1 }[/math] and [math]\displaystyle{ g_2 }[/math] that has more nodes than [math]\displaystyle{ g }[/math].