Connected Maximum Common Subgraph (cMCS)
Jump to navigation
Jump to search
A Connected Maximum Common Subgraph (cMCS) is a Maximum Common Subgraph (MCS) that consists of single subgraph, i.e. every vertex is connected to every other vertex by at least one path in the graph.
- Context:
- It can be mapped using a Connected Maximum Common Subgraph (cMCS) Algorithm.
- …
- Example(s):
- Counter-Example(s):
- See: Maximum Common Subgraph System, Maximum Common Subgraph Task, Graph Theory, Graph Edge, Graph Node.
References
2018
- (Duesbury et al., 2018) ⇒ Edmund Duesbury, John Holliday, and Peter Willett. (2018). “Comparison of Maximum Common Subgraph Isomorphism Algorithms for the Alignment of 2D Chemical Structures.” In: ChemMedChem Journal, 13(6). doi:10.1002/cmdc.201700482, PMID: 29057611
- QUOTE: There are two distinct types of MCS. The connected MCS (hereafter cMCS) represents the largest single fragment (in terms of either the number of atoms or the number of bonds) common to two compounds when they are aligned; whereas the disconnected MCS (hereafter dMCS) can contain multiple fragments and is the set of fragments that maximises the number of atoms or bonds in the MCS. The connected and disconnected forms of the MCS are illustrated in Figure 1. There are two additional subdivisions of the MCS: the maximum common edge‐induced subgraph (MCES) representing all the edges (i.e., bonds) between two graphs; and the maximum common node‐induced subgraph (MCIS) representing the nodes (i.e., atoms) in common between two graphs with their respective end‐points preserved.
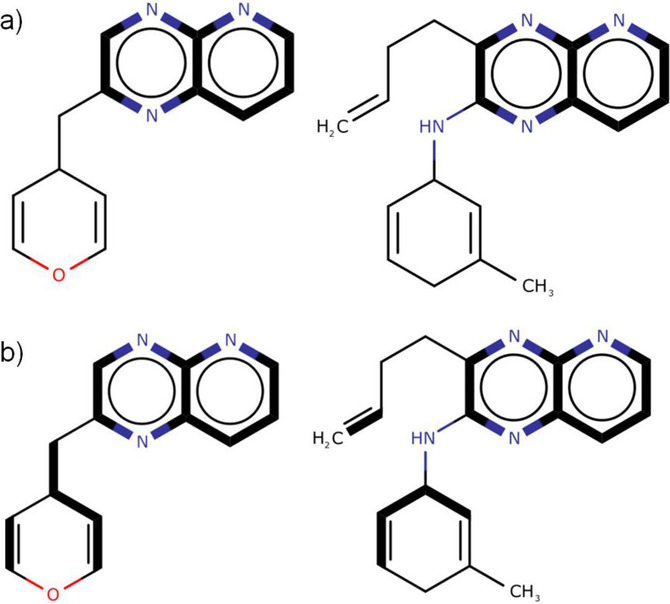
Figure 1. Types of MCES (the MCS in each pair of compounds represented by bold edges): a) cMCS between the two molecular graphs; b) dMCS between the same two molecular graphs.
- QUOTE: There are two distinct types of MCS. The connected MCS (hereafter cMCS) represents the largest single fragment (in terms of either the number of atoms or the number of bonds) common to two compounds when they are aligned; whereas the disconnected MCS (hereafter dMCS) can contain multiple fragments and is the set of fragments that maximises the number of atoms or bonds in the MCS. The connected and disconnected forms of the MCS are illustrated in Figure 1. There are two additional subdivisions of the MCS: the maximum common edge‐induced subgraph (MCES) representing all the edges (i.e., bonds) between two graphs; and the maximum common node‐induced subgraph (MCIS) representing the nodes (i.e., atoms) in common between two graphs with their respective end‐points preserved.
2002
- (Raymond & Willett, 2002) ⇒ John W. Raymond, and Peter Willett. (2002). “Maximum Common Subgraph Isomorphism Algorithms for the Matching of Chemical Structures.” In: Journal of Computer-Aided Molecular Design, 16. doi:https://doi.org/10.1023/A:1021271615909
- QUOTE: The MCS between two graphs can be classified further by distinguishing between the connected and disconnected case. A connected MCS is an MCS whereby each vertex is connected to every other vertex by at least one path in the graph (i.e., the MCS consists of a single subgraph). A disconnected MCS is comprised of two or more subgraph components. Figure 2(a) depicts the connected MCES between two molecular graphs, and Figure 2(b) illustrates the disconnected MCES between the same two molecular graphs. In general, a MCS between a pair of graphs is not necessarily unique as there may be more than one MCS.

