Maximum Common Induced Subgraph (MCIS)
A Maximum Common Induced Subgraph (MCIS) is a Maximum Common Subgraph that is an induced graph of two graphs in which their common nodes in common their respective end‐points are preserved.
- Context:
- It can be mapped by using a Maximum Common Induced Subgraph (MCIS) Algorithm.
- It ranges from being a Connected Maximum Common Induced Subgraph to being a Disconnected Maximum Common Induced Subgraph.
- Example(s):
- Counter-Example(s)
- See: Pharmacophore, Graph Theory, Theoretical Computer Science, Induced Subgraph, NP-Hard, Decision Problem, NP-Complete, Michael R. Garey, David S. Johnson, Computers And Intractability: A Guide to The Theory of NP-Completeness, Subgraph Isomorphism Problem, Hardness of Approximation.
References
2018a
- (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Maximum_common_subgraph Retrieved:2018-11-20.
- In graph theory and theoretical computer science, a maximum common subgraph may mean either:
- Maximum common induced subgraph, a graph that is an induced subgraph of two given graphs and has as many vertices as possible.
- Maximum common edge subgraph, a graph that is a subgraph of two given graphs and has as many edges as possible.
- In graph theory and theoretical computer science, a maximum common subgraph may mean either:
2018b
- (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Maximum_common_induced_subgraph Retrieved:2018-11-25.
- In graph theory and theoretical computer science, a maximum common induced subgraph of two graphs G and H is a graph that is an induced subgraph of both G and H,
and that has as many vertices as possible.
Finding this graph is NP-hard. In the associated decision problem, the input is two graphs G and H and a number k. The problem is to decide whether G and H have a common induced subgraph with at least k vertices. This problem is NP-complete. [1] It is a generalization of the induced subgraph isomorphism problem, which arises when k equals the number of vertices in the smaller of G and H, so that this entire graph must appear as an induced subgraph of the other graph. Based on hardness of approximation results for the maximum independent set problem, the maximum common induced subgraph problem is also hard to approximate. [2]. This implies that, unless P = NP, there is no approximation algorithm that, in polynomial time on [math]\displaystyle{ n }[/math] -vertex graphs, always finds a solution within a factor of [math]\displaystyle{ n^{1-\epsilon} }[/math] of optimal, for any [math]\displaystyle{ \epsilon \gt 0 }[/math] [3]. One possible solution for this problem is to build a modular product graph of G and H. In this graph, the largest clique corresponds to a maximum common induced subgraph of G and H. Therefore, algorithms for finding maximum cliques can be used to find the maximum common induced subgraph[4]. Maximum common induced subgraph algorithms have a long tradition in cheminformatics and pharmacophore mapping [5].
- In graph theory and theoretical computer science, a maximum common induced subgraph of two graphs G and H is a graph that is an induced subgraph of both G and H,
- ↑ Michael R. Garey and David S. Johnson (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1045-5 A1.4: GT48, pg.202.
- ↑ Kann, Viggo (1992), "On the approximability of the maximum common subgraph problem", STACS 92: 9th Annual Symposium on Theoretical Aspects of Computer Science Cachan, France, February 13–15, 1992, Proceedings, Lecture Notes in Computer Science, 577, Springer Science $\mathplus$ Business Media, pp. 375–388, doi:10.1007/3-540-55210-3_198.
- ↑ Zuckerman, D. (2006), "Linear degree extractors and the inapproximability of max clique and chromatic number", Proc. 38th ACM Symp. Theory of Computing, pp. 681–690, doi:10.1145/1132516.1132612, ISBN 1-59593-134-1, ECCC TR05-100.
- ↑ Barrow, H.; Burstall, R. (1976), "Subgraph isomorphism, matching relational structures and maximal cliques", Information Processing Letters, 4 (4): 83–84, doi:10.1016/0020-0190(76)90049-1.
- ↑ Raymond, John W.; Willett, Peter (2002)
2018c
- (Duesbury et al., 2018) ⇒ Edmund Duesbury, John Holliday, and Peter Willett. (2018). “Comparison of Maximum Common Subgraph Isomorphism Algorithms for the Alignment of 2D Chemical Structures.” In: ChemMedChem Journal, 13(6). doi:10.1002/cmdc.201700482, PMID: 29057611
- QUOTE: There are two distinct types of MCS. The connected MCS (hereafter cMCS) represents the largest single fragment (in terms of either the number of atoms or the number of bonds) common to two compounds when they are aligned; whereas the disconnected MCS (hereafter dMCS) can contain multiple fragments and is the set of fragments that maximises the number of atoms or bonds in the MCS. The connected and disconnected forms of the MCS are illustrated in Figure 1. There are two additional subdivisions of the MCS: the maximum common edge‐induced subgraph (MCES) representing all the edges (i.e., bonds) between two graphs; and the maximum common node‐induced subgraph (MCIS) representing the nodes (i.e., atoms) in common between two graphs with their respective end‐points preserved.
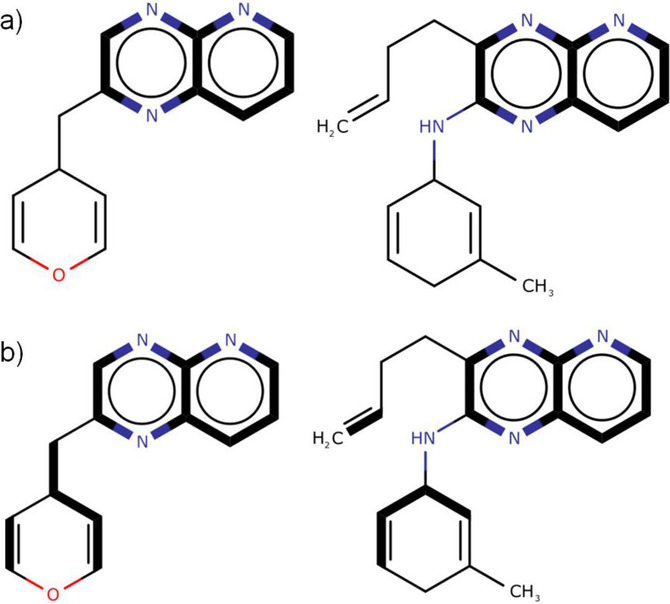
Figure 1. Types of MCES (the MCS in each pair of compounds represented by bold edges): a) cMCS between the two molecular graphs; b) dMCS between the same two molecular graphs.
- QUOTE: There are two distinct types of MCS. The connected MCS (hereafter cMCS) represents the largest single fragment (in terms of either the number of atoms or the number of bonds) common to two compounds when they are aligned; whereas the disconnected MCS (hereafter dMCS) can contain multiple fragments and is the set of fragments that maximises the number of atoms or bonds in the MCS. The connected and disconnected forms of the MCS are illustrated in Figure 1. There are two additional subdivisions of the MCS: the maximum common edge‐induced subgraph (MCES) representing all the edges (i.e., bonds) between two graphs; and the maximum common node‐induced subgraph (MCIS) representing the nodes (i.e., atoms) in common between two graphs with their respective end‐points preserved.
2002
- (Raymond & Willett, 2002) ⇒ John W. Raymond, and Peter Willett. (2002). “Maximum Common Subgraph Isomorphism Algorithms for the Matching of Chemical Structures.” In: Journal of Computer-Aided Molecular Design, 16. doi:https://doi.org/10.1023/A:1021271615909
- QUOTE: Two graphs are said to be isomorphic if there is a one-to-one correspondence between their vertices and an edge only exists between two vertices in one graph if an edge exists between the two corresponding vertices in the other graph. An induced subgraph is a set [math]\displaystyle{ S }[/math] of vertices of a graph [math]\displaystyle{ G }[/math] and those edges of [math]\displaystyle{ G }[/math] with both end-points in [math]\displaystyle{ S }[/math]. A graph [math]\displaystyle{ G_{12} }[/math] is a common induced subgraph of graphs [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] if [math]\displaystyle{ G_{12} }[/math] is isomorphic to induced subgraphs of [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math]. A maximum common induced subgraph (MCIS) consists of a graph [math]\displaystyle{ G_{12} }[/math] with the largest number of vertices meeting the aforementioned property. Related to the MCIS is the maximum common edge subgraph (MCES). An MCES is a subgraph consisting of the largest number of edges common to both [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math]. In this treatment, the term MCS will be used to denote both the MCIS and MCES problems.
Figure 1(a) illustrates an MCIS between two graphs (highlighted in bold), and Figure 1(b) demonstrates an MCES between the same two graphs. It is clear from Figure 1(b) that the MCES between the two graphs is simply the common subgraph with the largest number of edges. The MCIS in Figure 1(a) is less intuitive. The MCIS consists of the common subgraph with the largest number of vertices under the constraint that every edge present in graph [math]\displaystyle{ G_1(G_2) }[/math] that is incident on a vertex contained in the MCIS must also have a corresponding edge in the other graph [math]\displaystyle{ G_2(G_1) }[/math]. For instance, in the MCES, vertex 4 in graph [math]\displaystyle{ G_1 }[/math] maps to vertex 3' in graph [math]\displaystyle{ G_2 }[/math] because edges (3,4), (4,5), and (4,7) in [math]\displaystyle{ G_1 }[/math] correspond to edges (2' ,3' ), (3' ,4'), and (3',7' ) in [math]\displaystyle{ G_2 }[/math], respectively. In the MCIS, however, vertex 4 in [math]\displaystyle{ G_1 }[/math] does not match to vertex 3' in [math]\displaystyle{ G_2 }[/math], because there is an edge, (2,4), incident on vertex 4 in [math]\displaystyle{ G_1 }[/math] that does not have a corresponding edge incident on vertex 3' in [math]\displaystyle{ G_2. }[/math]
- QUOTE: Two graphs are said to be isomorphic if there is a one-to-one correspondence between their vertices and an edge only exists between two vertices in one graph if an edge exists between the two corresponding vertices in the other graph. An induced subgraph is a set [math]\displaystyle{ S }[/math] of vertices of a graph [math]\displaystyle{ G }[/math] and those edges of [math]\displaystyle{ G }[/math] with both end-points in [math]\displaystyle{ S }[/math]. A graph [math]\displaystyle{ G_{12} }[/math] is a common induced subgraph of graphs [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] if [math]\displaystyle{ G_{12} }[/math] is isomorphic to induced subgraphs of [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math]. A maximum common induced subgraph (MCIS) consists of a graph [math]\displaystyle{ G_{12} }[/math] with the largest number of vertices meeting the aforementioned property. Related to the MCIS is the maximum common edge subgraph (MCES). An MCES is a subgraph consisting of the largest number of edges common to both [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math]. In this treatment, the term MCS will be used to denote both the MCIS and MCES problems.

