Neural Network Forward Pass
A Neural Network Forward Pass is a Forward Propagation Algorithm that feeds input values into the neural network and computes the output predicted values.
- AKA: Neural Network Forward State.
- Example(s):
- Counter-Example(s):
- See: Bidirectional Neural Network, ConvNet Network, RNN Network.
References
2018a
- (CS231n, 2018) ⇒http://cs231n.github.io/neural-networks-1/#feedforward Retrieved: 2018-07-15.
- QUOTE: The full forward pass of this 3-layer neural network is then simply three matrix multiplications, interwoven with the application of the activation function:
f = lambda x: 1.0/( 1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)
- In the above code,
W1,W2,W3,b1,b2,b3are the learnable parameters of the network.
- In the above code,
2018b
- (Wikipedia, 2018) ⇒ https://www.wikiwand.com/en/Backpropagation#Pseudocode Retrieved: 2018-07-15.
- The following is pseudocode for a stochastic gradient descent algorithm for training a three-layer network (only one hidden layer):
do
forEach training example named ex
prediction = neural-net-output(network, ex) // forward pass
actual = teacher-output(ex)
compute error (prediction - actual) at the output units
compute [math]\displaystyle{ \Delta w_h }[/math] for all weights from hidden layer to output layer // backward pass
compute [math]\displaystyle{ \Delta w_i }[/math] for all weights from input layer to hidden layer // backward pass continued update network weights // input layer not modified by error estimate
until all examples classified correctly or another stopping criterion satisfied
return the network
- The lines labeled "backward pass" can be implemented using the backpropagation algorithm, which calculates the gradient of the error of the network regarding the network's modifiable weights.[1]
2018c
- (Raven Protocol, 2018) ⇒ "Forward propagation" In: https://medium.com/ravenprotocol/everything-you-need-to-know-about-neural-networks-6fcc7a15cb4 Retrieved: 2018-07-15
- QUOTE: Forward propagation is a process of feeding input values to the neural network and getting an output which we call predicted value. Sometimes we refer forward propagation as inference. When we feed the input values to the neural network’s first layer, it goes without any operations. Second layer takes values from first layer and applies multiplication, addition and activation operations and passes this value to the next layer. Same process repeats for subsequent layers and finally we get an output value from the last layer.
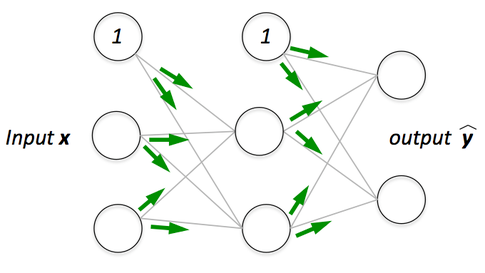
Forward Propagation
- QUOTE: Forward propagation is a process of feeding input values to the neural network and getting an output which we call predicted value. Sometimes we refer forward propagation as inference. When we feed the input values to the neural network’s first layer, it goes without any operations. Second layer takes values from first layer and applies multiplication, addition and activation operations and passes this value to the next layer. Same process repeats for subsequent layers and finally we get an output value from the last layer.
2016
- (wang, 2016) ⇒ Tingwu Wang (2016) Recurrent Neural Network Tutorial: http://www.cs.toronto.edu/~tingwuwang/rnn_tutorial.pdf
- QUOTE: 1. Algorithm looks like this:.
2015
- (Urtasun & Zemel, 2015]]) ⇒ Raquel Urtasun, and Rich Zemel (2015). CSC 411: Lecture 10: Neural Networks I"
- QUOTE: We only need to know two algorithms:
- Forward pass: performs inference.
- Backward pass: performs learning
- QUOTE: We only need to know two algorithms:
2005
- (Graves & Schmidhuber, 2005) ⇒ Alex Graves and Jurgen Schmidhuber (2005). "Framewise phoneme classification with bidirectional LSTM and other neural network architectures" (PDF). Neural Networks, 18(5-6), 602-610. DOI 10.1016/j.neunet.2005.06.042
- QUOTE: Forward Pass
- Reset all activations to 0.
- Running forwards from time [math]\displaystyle{ \tau_0 }[/math]to time [math]\displaystyle{ \tau_1 }[/math], feed in the inputs and update the activations. Store all hidden layer and output activations at every timestep.
- For each LSTM block, the activations are updated as follows:
Input Gates: [math]\displaystyle{ x_l =\sum_{j \in N} w_{lj} y_j (\tau − 1) + \sum_{c in C}w_{lc}s_c(\tau − 1) \;,\; \quad y_l = f(x_l) }[/math]
Forget Gates: [math]\displaystyle{ x_phi =\sum_{j \in N} w_{\phi j}y_j (\tau − 1) + \sum_{c\in C}w_{\phi c}s_c(\tau − 1) \;,\; \quad y_\phi = f(x_\phi) }[/math]
Cells: [math]\displaystyle{ \forall_{c \in C}, x_c =\sum_{j\in N} w_{cj}y_j (\tau − 1)\;,\; \quad s_c = y_\phi s_c(\tau − 1) + y_lg(x_c) }[/math]
Output Gates: [math]\displaystyle{ x_w =\sum_{j\in N}w_{wj}y_j (\tau − 1) + \sum_{c\in C} w_{wc}s_c(\tau)\;,\; \quad y_w = f(x_w) }[/math]
Cell Outputs: [math]\displaystyle{ \forall_{c \in C}, y_c = y_wh(s_c) }[/math]
- QUOTE: Forward Pass
1997
- (Schuster & Paliwal, 1997) ⇒ Mike Schuster, and Kuldip K. Paliwal. (1997). “Bidirectional Recurrent Neural Networks.” In: IEEE Transactions on Signal Processing Journal, 45(11). doi:10.1109/78.650093
- QUOTE: To overcome the limitations of a regular RNN outlined in the previous section, we propose a bidirectional recurrent neural network (BRNN) that can be trained using all available input information in the past and future of a specific time frame.
1) Structure: The idea is to split the state neurons of a regular RNN in a part that is responsible for the positive time direction (forward states) and a part for the negative time direction (backward states). Outputs from forward states are not connected to inputs of backward states, and vice versa. This leads to the general structure that can be seen in Fig. 3, where it is unfolded over three time steps.
.
Fig. 3. General structure of the bidirectional recurrent neural network (BRNN) shown unfolded in time for three time steps
(...) The training procedure for the unfolded bidirectional network over time can be summarized as follows.
- QUOTE: To overcome the limitations of a regular RNN outlined in the previous section, we propose a bidirectional recurrent neural network (BRNN) that can be trained using all available input information in the past and future of a specific time frame.
- 1) FORWARD PASS
- Run all input data for one time slice [math]\displaystyle{ 1 \lt t \leq T }[/math]through the BRNN and determine all predicted outputs.
- a) Do forward pass just for forward states (from [math]\displaystyle{ t=1 }[/math] to [math]\displaystyle{ t=T }[/math]) and backward states (from [math]\displaystyle{ t=T }[/math] to [math]\displaystyle{ t=1 }[/math]).
- b) Do forward pass for output neurons.
- 2) BACKWARD PASS
- Calculate the part of the objective function derivative for the time slice [math]\displaystyle{ 1 \lt t \leq T }[/math] used in the forward pass.
- a) Do backward pass for output neurons.
- b) Do backward pass just for forward states (from [math]\displaystyle{ t=T }[/math] to [math]\displaystyle{ t=1 }[/math]) and backward states (from [math]\displaystyle{ t=1 }[/math] to [math]\displaystyle{ t=T }[/math]).
- 3) UPDATE WEIGHTS
