Neural Network Backward Pass

From GM-RKB
Jump to navigation Jump to search

A Neural Network Backward Pass is a Back-Propagation Algorithm that defines a Neural Network Hidden Layer that represents the state of backpropagation.

References

2018

initialize network weights (often small random values)

do

forEach training example named ex

prediction = neural-net-output(network, ex) // forward pass

actual = teacher-output(ex)

compute error (prediction - actual) at the output units

compute [math]\displaystyle{ \Delta w_h }[/math] for all weights from hidden layer to output layer // backward pass

compute [math]\displaystyle{ \Delta w_i }[/math] for all weights from input layer to hidden layer // backward pass continued update network weights // input layer not modified by error estimate

until all examples classified correctly or another stopping criterion satisfied

return the network

The lines labeled "backward pass" can be implemented using the backpropagation algorithm, which calculates the gradient of the error of the network regarding the network's modifiable weights.[1]

2018c

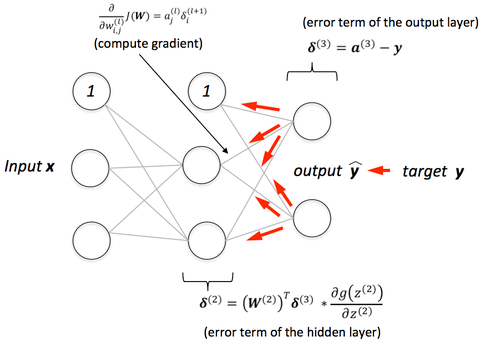
Backward Propagation

2016

2015

2005

  • (Graves & Schmidhuber, 2005) ⇒ Alex Graves and Jurgen Schmidhuber (2005). "Framewise phoneme classification with bidirectional LSTM and other neural network architectures" (PDF). Neural Networks, 18(5-6), 602-610. DOI 10.1016/j.neunet.2005.06.042
    • QUOTE: Backward Pass
      • Reset all partial derivatives to 0.
      • Starting at time [math]\displaystyle{ \tau_1 }[/math], propagate the output errors backwards through the unfolded net, using the standard BPTT equations for a softmax output layer and the cross-entropy error function:

        [math]\displaystyle{ define\; \delta_k(\tau)=\frac{\partial E(\tau)}{\partial x_k}; \quad \delta_k(\tau) = y_k(\tau ) − t_k(\tau)\quad k \in \text{output units} }[/math]

        *** For each LSTM block the δ’s are calculated as follows:

        Cell Outputs: [math]\displaystyle{ \forall c \in C,\; define\, \epsilon = \sum_{j\in N}w_{jc}\delta_j (\tau + 1) }[/math]

        Output Gates: [math]\displaystyle{ \delta_w = f'(x_w)\sum_{c\in C}\epsilon_c h(s_c) }[/math]

        States: [math]\displaystyle{ \frac{\partial E}{\partial s_c}(\tau)=\epsilon_c y_w h'(s_c)+\frac{\partial E}{\partial s_c}(\tau+1)y_\phi (\tau+1)+\delta_l(\tau + 1)w_{lc} + \delta_\phi(\tau + 1)w_{\phi c} + \delta _ww_{wc} }[/math]

        Cells: [math]\displaystyle{ \forall c \in C, \delta_c = y_{l}g'(x_c)\frac{\partial E}{\partial s_c} }[/math]

        Forget Gates:[math]\displaystyle{ \delta_\phi = f'(x_phi)\sum_{c\in C}\frac{\partial E}{\partial s_c} s_c(\tau -1) }[/math]

        Input Gates: [math]\displaystyle{ \delta_l = f'(x_l)\sum_{c\in C}\frac{\partial E}{\partial s_c} g(x_c) }[/math]

      • Using the standard BPTT equation, accumulate the δ’s to get the partial derivatives of the cumulative sequence error: [math]\displaystyle{ define\; E_{total}(S) = \sum^{\tau_1}_{\tau=\tau_0} E(\tau);\quad define\; \bigtriangledown_{ij} (S) = \frac{\partial E_{total}(S)}{\partial w_{ij}} \implies \bigtriangledown_{ij} (S)= \sum^{\tau_1}_{\tau=\tau_0+1} \delta_i(\tau)y_j (\tau − 1) }[/math]

1997

1) FORWARD PASS
Run all input data for one time slice [math]\displaystyle{ 1 \lt t \leq T }[/math]through the BRNN and determine all predicted outputs.
a) Do forward pass just for forward states (from [math]\displaystyle{ t=1 }[/math] to [math]\displaystyle{ t=T }[/math]) and backward states (from [math]\displaystyle{ t=T }[/math] to [math]\displaystyle{ t=1 }[/math]).
b) Do forward pass for output neurons.
2) BACKWARD PASS
Calculate the part of the objective function derivative for the time slice [math]\displaystyle{ 1 \lt t \leq T }[/math] used in the forward pass.
a) Do backward pass for output neurons.
b) Do backward pass just for forward states (from [math]\displaystyle{ t=T }[/math] to [math]\displaystyle{ t=1 }[/math]) and backward states (from [math]\displaystyle{ t=1 }[/math] to [math]\displaystyle{ t=T }[/math]).
3) UPDATE WEIGHTS
  1. ↑ Paul J. Werbos (1994). The Roots of Backpropagation. From Ordered Derivatives to Neural Networks and Political Forecasting. New York, NY: John Wiley & Sons, Inc.
Retrieved from "http://www.gabormelli.com/RKB/index.php?title=Neural_Network_Backward_Pass&oldid=841924"