Neural Network Batch Normalization Layer

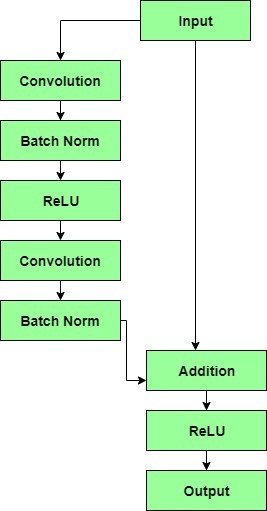
Counter-Example(s):
- Network Pooling Layer,
- Neural Network Convolution Layer.
See: Recurrent Neural Network, Convolution Operator, Convolutional Kernel Function.

References

(Howard & Ruder, 2018) ⇒ Jeremy Howard, and Sebastian Ruder. (2018). “Universal Language Model Fine-tuning for Text Classification.” In: Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (ACL-2018).
- QUOTE: ... for fine-tuning the classifier, we augment the pretrained language model with two additional linear blocks. Following standard practice for CV classifiers, each block uses batch normalization (Ioffe and Szegedy, 2015) and dropout, with ReLU activations for the intermediate layer and a softmax activation that outputs a probability distribution over target classes at the last layer.

(Goldberg, 2017) ⇒ Yoav Goldberg. (2017). “Neural Network Methods for Natural Language Processing.” In: Synthesis Lectures on Human Language Technologies, 10(1). doi:10.2200/S00762ED1V01Y201703HLT037
- QUOTE: ... Layer normalization is an effective measure for countering saturation, but is also expensive in terms of gradient computation. A related technique is batch normalization, due to Ioffe and Szegedy (2015), in which the activations at each layer are normalized so that they have mean 0 and variance 1 across each mini-batch. The batch-normalization techniques became a key component for effective training of deep networks in computer vision. As of this writing, it is less popular in natural language applications.

(Such et al., 2017) ⇒ Felipe Petroski Such, Vashisht Madhavan, Edoardo Conti, Joel Lehman, Kenneth O. Stanley, and Jeff Clune. (2017). “Deep Neuroevolution: Genetic Algorithms Are a Competitive Alternative for Training Deep Neural Networks for Reinforcement Learning.” In: arXiv:1712.06567
- QUOTE: ... The ES requires require virtual batch normalization to generate diverse policies amongst the pseudo-offspring, which is necessary for accurate finite difference approximation (Salimans et al., 2016). Virtual batch normalization requires additional forward passes for a reference batch – a random set of observations chosen at the start of training–to compute layer normalization statistics that are then used in the same manner as batch normalization (Ioffe & Szegedy, 2015). We found that the random GA parameter perturbations generate sufficiently diverse policies without virtual batch normalization and thus avoid these additional forward passes through the network.

(Ioffe & Szegedy, 2015) ⇒ Sergey Ioffe, and Christian Szegedy. (2015). “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift.” In: Proceedings of the International Conference on Machine Learning, pp. 448-456.
- ABSTRACT: Training Deep Neural Networks is complicated by the fact that the distribution of each layer's inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models with saturating nonlinearities. We refer to this phenomenon as internal covariate shift, and address the problem by normalizing layer inputs. Our method draws its strength from making normalization a part of the model architecture and performing the normalization for each training mini-batch. Batch Normalization allows us to use much higher learning rates and be less careful about initialization, and in some cases eliminates the need for Dropout. Applied to a state-of-the-art image classification model, Batch Normalization achieves the same accuracy with 14 times fewer training steps, and beats the original model by a significant margin. Using an ensemble of batch-normalized networks, we improve upon the best published result on ImageNet classification: reaching 4.82% top-5 test error, exceeding the accuracy of human raters.