Dilated Convolutional Neural Network
A Dilated Convolutional Neural Network is a convolutional neural network that ...
- See: DenseNet.
References
2017
- (Yang et al., 2017) ⇒ Zichao Yang, Zhiting Hu, Ruslan Salakhutdinov, and Taylor Berg-Kirkpatrick. (2017). “Improved Variational Autoencoders for Text Modeling Using Dilated Convolutions.” arXiv preprint arXiv:1702.08139
2016
- (Oord et al., 2016) ⇒ Van Den Oord, Aaron, Sander Dieleman, Heiga Zen, Karen Simonyan, Oriol Vinyals, Alex Graves, Nal Kalchbrenner, Andrew Senior, and Koray Kavukcuoglu. (2016). “Wavenet: A Generative Model for Raw Audio.” arXiv preprint arXiv:1609.03499
- QUOTE: … Figure 3: Visualization of a stack of dilated causal convolutional layers.
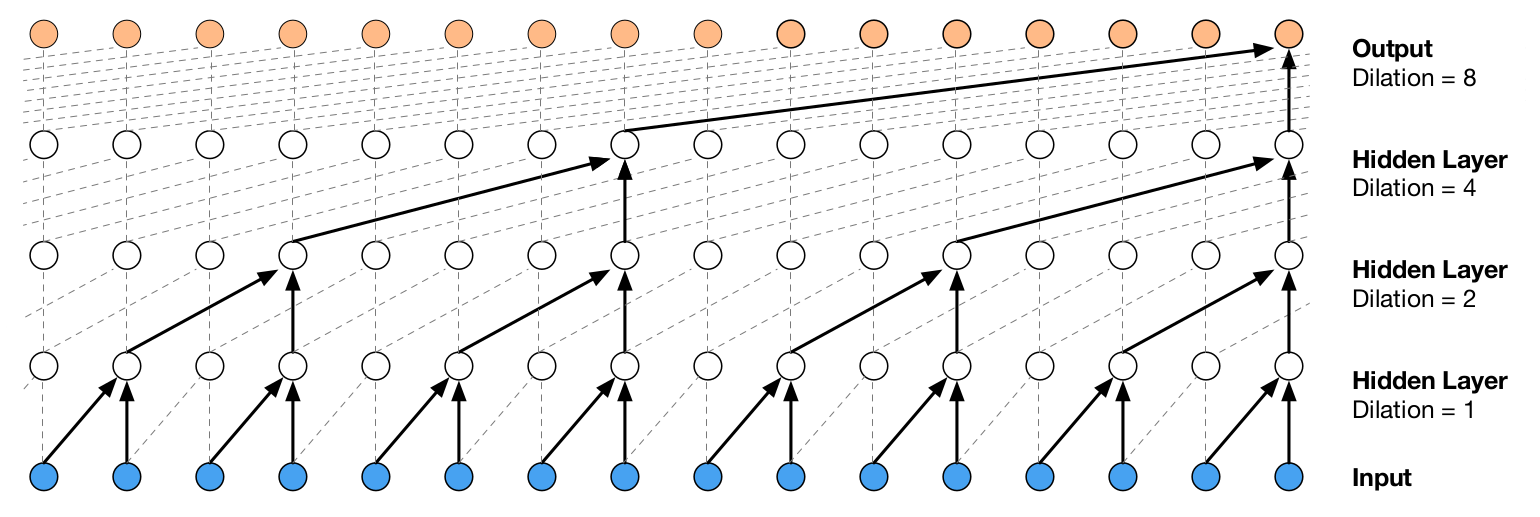
- QUOTE: … Figure 3: Visualization of a stack of dilated causal convolutional layers.
2015
- (Yu & Koltun, 2015) ⇒ Fisher Yu, and Vladlen Koltun. (2015). “Multi-scale Context Aggregation by Dilated Convolutions.” In: Proceedings of 4th International Conference on Learning Representations (ICLR-2016).
- QUOTE: The dilated convolution operator has been referred to in the past as “convolution with a dilated filter”. It plays a key role in the algorithme `a trous, an algorithm for wavelet decomposition (Holschneider et al., 1987; Shensa, 1992). [1]
We use the term “dilated convolution” instead of “convolution with a dilated filter” to clarify that no “dilated filter” is constructed or represented.
The convolution operator itself is modified to use the filter parameters in a different way. The dilated convolution operator can apply the same filter at different ranges using different dilation factors. Our definition reflects the proper implementation of the dilated convolution operator, which does not involve construction of dilated filters.
In recent work on convolutional networks for semantic segmentation, Long et al. (2015) analyzed filter dilation but chose not to use it. Chen et al. (2015a) used dilation to simplify the architecture of Long et al. (2015).
In contrast, we develop a new convolutional network architecture that systematically uses dilated convolutions for multi-scale context aggregation. …
- QUOTE: The dilated convolution operator has been referred to in the past as “convolution with a dilated filter”. It plays a key role in the algorithme `a trous, an algorithm for wavelet decomposition (Holschneider et al., 1987; Shensa, 1992). [1]
- ↑ ! R be discrete 3�3 filters. Consider applying the filters with exponentially increasing dilation: Fi+1 = Fi �2i ki for i = 0; 1; : : : ; n 2: (3)