Chebyshev Polynomial
(Redirected from Chebyshev polynomials)
Jump to navigation
Jump to search
A Chebyshev Polynomial is a trigonometric function that defines two polynomials sequences related to the cosine and sine functions.
- Context:
- It is a special case of the Gegenbauer Polynomial.
- It can be evaluated by a Clenshaw Algorithm.
- Example(s):
- Counter-Example(s):
- See: Transliteration, Orthogonal Functions, Chebyshev Equation, Sturm–Liouville Problem, Chebyshev Nodes, Polynomial Interpolation, Chebyshev Differential Equation, Chebyshev Integral, Chebyshev's Theorem, Chebyshev Function.
References
2021a
- (MathWolfram, 2021) ⇒ Eric W. Weisstein (2021) "Chebyshev Polynomial of the First Kind". In: MathWorld--A Wolfram Web Resource.
- QUOTE: The Chebyshev polynomials of the first kind are a set of orthogonal polynomials defined as the solutions to the Chebyshev differential equation and denoted $T_n(x)$. They are used as an approximation to a least squares fit, and are a special case of the Gegenbauer polynomial with $\alpha=0$. They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the first kind are denoted $T_n(x)$, and are implemented in the Wolfram Language as ChebyshevT$[n, x]$. They are normalized such that $T_n(1)=1$. The first few polynomials are illustrated above for $x$ in $[-1,1]$ and $n=1, 2, \ldots, 5$. .
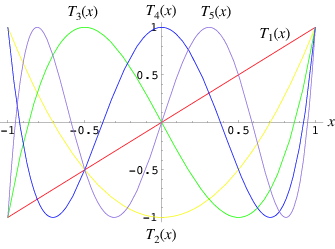
- QUOTE: The Chebyshev polynomials of the first kind are a set of orthogonal polynomials defined as the solutions to the Chebyshev differential equation and denoted $T_n(x)$. They are used as an approximation to a least squares fit, and are a special case of the Gegenbauer polynomial with $\alpha=0$. They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the first kind are denoted $T_n(x)$, and are implemented in the Wolfram Language as ChebyshevT$[n, x]$. They are normalized such that $T_n(1)=1$. The first few polynomials are illustrated above for $x$ in $[-1,1]$ and $n=1, 2, \ldots, 5$.
2021b
- (MathWolfram, 2021) ⇒ Eric W. Weisstein (2021) "Chebyshev Polynomial of the Second Kind"]. In: MathWorld--A Wolfram Web Resource.
- QUOTE: A modified set of Chebyshev polynomials defined by a slightly different generating function. They arise in the development of four-dimensional spherical harmonics in angular momentum theory. They are a special case of the Gegenbauer polynomial with $\alpha=1$. They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the second kind are denoted $U_n(x)$, and implemented in the Wolfram Language as ChebyshevU$[n, x]$. The polynomials $U_n(x)$ are illustrated above for $x$ in $[-1,1]$ and $n=1, 2, \ldots, 5$. .
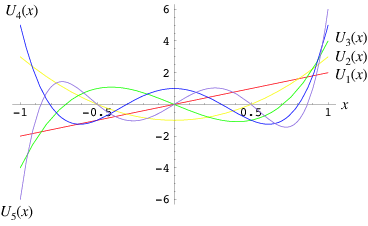
- QUOTE: A modified set of Chebyshev polynomials defined by a slightly different generating function. They arise in the development of four-dimensional spherical harmonics in angular momentum theory. They are a special case of the Gegenbauer polynomial with $\alpha=1$. They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the second kind are denoted $U_n(x)$, and implemented in the Wolfram Language as ChebyshevU$[n, x]$. The polynomials $U_n(x)$ are illustrated above for $x$ in $[-1,1]$ and $n=1, 2, \ldots, 5$.
2021c
- (Wikipedia, 2021) ⇒ https://en.wikipedia.org/wiki/Chebyshev_polynomials Retrieved:2021-8-29.
- The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as [math]\displaystyle{ T_n(x) }[/math] and [math]\displaystyle{ U_n(x) }[/math]. They can be defined several ways that have the same end result; in this article the polynomials are defined by starting with trigonometric functions:
- The Chebyshev polynomials of the first kind [math]\displaystyle{ T_n }[/math] are given by
- [math]\displaystyle{ T_n\left(\cos{\theta}\right)=\cos{(n\theta)}. }[/math]
- Similarly, define the Chebyshev polynomials of the second kind [math]\displaystyle{ U_n }[/math] as
- [math]\displaystyle{ U_n\left(\cos{\theta}\right)\sin{\theta}=\sin{\big(\big(n+1)\theta\big)}. }[/math]
- The Chebyshev polynomials of the first kind [math]\displaystyle{ T_n }[/math] are given by
- These definitions do not appear to be polynomials, but by using various trigonometric identities they can be converted to an explicitly polynomial form. For example, for n = 2 the T2 formula can be converted into a polynomial with argument x = cos(θ), using the double angle formula:
- [math]\displaystyle{ \cos(2\theta) = 2\cos^2(\theta) - 1. }[/math]
- Replacing the terms in the formula with the definitions above, we get
- [math]\displaystyle{ T_2(x) = 2x^2 - 1. }[/math]
- The other Tn(x) are defined similarly, where for the polynomials of the second kind (Un) we must use de Moivre's formula to get sin(n θ) as sin(θ) times a polynomial in cos(θ) . For instance,
- [math]\displaystyle{ \sin(3 \theta) = (4 \cos^2(\theta) - 1)\, \sin(\theta) }[/math]
- gives
- [math]\displaystyle{ U_2(x) = 4x^2 - 1. }[/math]
- Once converted to polynomial form, Tn(x) and Un(x) are called Chebyshev polynomials of the first and second kind, respectively.
- Conversely, an arbitrary integer power of trigonometric functions may be expressed as a linear combination of trigonometric functions using Chebyshev polynomials
- [math]\displaystyle{ \cos^n\! \theta = 2^{1-n}\!\mathop{\mathop{{\sum}'}^n_{j=0}}_{n-j\,\mathrm{even}}\!\! \binom{n}{\tfrac{n-j}{2}}\,T_j(\cos \theta), }[/math]
- where the prime at the sum symbol indicates that the contribution of j = 0 needs to be halved if it appears, and [math]\displaystyle{ T_j(\cos \theta)=\cos j\theta }[/math].
- An important and convenient property of the Tn(x) is that they are orthogonal with respect to the inner product
- [math]\displaystyle{ \langle f,g\rangle~=~\int_{-1}^1\,f(x)\,g(x)\,\frac{\mathrm{d}x}{\,\sqrt{1 - x^2\,}\,}~, }[/math]
- and Un(x) are orthogonal with respect to another, analogous inner product product, given below.
- This follows from the fact that the Chebyshev polynomials solve the Chebyshev differential equations
- [math]\displaystyle{ (1 - x^2)\,y'' - x\,y' + n^2\,y = 0~, }[/math]
- [math]\displaystyle{ (1 - x^2)\,y'' - 3\,x\,y' + n\,(n + 2)\,y = 0~, }[/math]
- which are Sturm–Liouville differential equations. It is a general feature of such differential equations that there is a distinguished orthonormal set of solutions. (Another way to define the Chebyshev polynomials is as the solutions to those equations.)
- The Chebyshev polynomials Tn are polynomials with the largest possible leading coefficient, whose absolute value on the interval [−1, 1] is bounded by 1. They are also the "extremal" polynomials for many other properties.[1]
- Chebyshev polynomials are important in approximation theory because the roots of Tn(x), which are also called Chebyshev nodes, are used as matching-points for optimizing polynomial interpolation. The resulting interpolation polynomial minimizes the problem of Runge's phenomenon, and provides an approximation that is close to the best polynomial approximation to a continuous function under the maximum norm, also called the “minimax” criterion. This approximation leads directly to the method of Clenshaw–Curtis quadrature.
- These polynomials were named after Pafnuty Chebyshev.[2] The letter T is used because of the alternative transliterations of the name Chebyshev as Tchebycheff, Tchebyshev (French) or Tschebyschow (German).
- ↑ Rivlin, Theodore J. (1974). "Chapter 2, Extremal properties". The Chebyshev Polynomials. Pure and Applied Mathematics (1st ed.). New York-London-Sydney: Wiley-Interscience [John Wiley & Sons]. pp. 56–123. ISBN 978-047172470-4.
- ↑ Chebyshev polynomials were first presented in Chebyshev, P. L. (1854). "Théorie des mécanismes connus sous le nom de parallélogrammes". Mémoires des Savants étrangers présentés à l'Académie de Saint-Pétersbourg 7: 539–586.