Chebyshev Polynomial of the First Kind

A Chebyshev Polynomial of the First Kind is a Chebyshev Polynomial that is a special case of the Gegenbauer Polynomial ($\alpha=0$).

• Context:
  • It is usually denoted $T_n(x)$.
  • It can be used as an approximation to a least squares fit.
  • It can be orthogonal polynomials defined as the solutions to the Chebyshev differential equation.
  • It can be evaluated by a Clenshaw Algorithm.
• Example(s):
  • $T_0(x) = 1$,
  • $T_1(x) = x$,
  • $T_2(x) = 2x^2 - 1 $,
  • $T_3(x) = 4x^3 - 3x$,
  • $T_4(x) = 8x^4 - 8x^2 + 1$,
  • …
• Counter-Example(s):
  • a Chebyshev Polynomial of the Second Kind.
• See: Transliteration, Orthogonal Functions, Chebyshev Equation, Sturm–Liouville Problem, Chebyshev Nodes, Polynomial Interpolation, Chebyshev Differential Equation, Chebyshev Integral, Chebyshev's Theorem, Chebyshev Function.

---

---

References

2021a

• (MathWolfram, 2021) ⇒ Eric W. Weisstein (2021) "Chebyshev Polynomial of the First Kind". In: MathWorld--A Wolfram Web Resource.
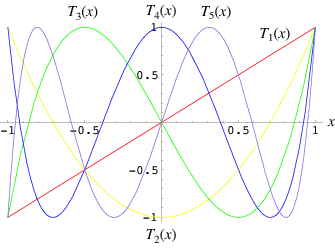
  • QUOTE: The Chebyshev polynomials of the first kind are a set of orthogonal polynomials defined as the solutions to the Chebyshev differential equation and denoted $T_n(x)$. They are used as an approximation to a least squares fit, and are a special case of the Gegenbauer polynomial with $\alpha=0$. They are also intimately connected with trigonometric multiple-angle formulas. The Chebyshev polynomials of the first kind are denoted $T_n(x)$, and are implemented in the Wolfram Language as ChebyshevT$[n, x]$. They are normalized such that $T_n(1)=1$. The first few polynomials are illustrated above for $x$ in $[-1,1]$ and $n=1, 2, \ldots, 5.
    
    .

2021b

• (Wikipedia, 2021) ⇒ https://en.wikipedia.org/wiki/Chebyshev_polynomials Retrieved:2021-8-29.
  • The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as [math]\displaystyle{ T_n(x) }[/math] and [math]\displaystyle{ U_n(x) }[/math]. They can be defined several ways that have the same end result; in this article the polynomials are defined by starting with trigonometric functions:

The Chebyshev polynomials of the first kind [math]\displaystyle{ T_n }[/math] are given by

[math]\displaystyle{ T_n\left(\cos{\theta}\right)=\cos{(n\theta)}. }[/math]

Similarly, define the Chebyshev polynomials of the second kind [math]\displaystyle{ U_n }[/math] as

[math]\displaystyle{ U_n\left(\cos{\theta}\right)\sin{\theta}=\sin{\big(\big(n+1)\theta\big)}. }[/math]

These definitions do not appear to be polynomials, but by using various trigonometric identities they can be converted to an explicitly polynomial form. For example, for n = 2 the T₂ formula can be converted into a polynomial with argument x = cos(θ), using the double angle formula:

[math]\displaystyle{ \cos(2\theta) = 2\cos^2(\theta) - 1. }[/math]

Replacing the terms in the formula with the definitions above, we get

[math]\displaystyle{ T_2(x) = 2x^2 - 1. }[/math]

The other T_n(x) are defined similarly, where for the polynomials of the second kind (U_n) we must use de Moivre's formula to get sin(n θ) as sin(θ) times a polynomial in cos(θ) . For instance,

[math]\displaystyle{ \sin(3 \theta) = (4 \cos^2(\theta) - 1)\, \sin(\theta) }[/math]

gives

[math]\displaystyle{ U_2(x) = 4x^2 - 1. }[/math]

Once converted to polynomial form, T_n(x) and U_n(x) are called Chebyshev polynomials of the first and second kind, respectively.

Conversely, an arbitrary integer power of trigonometric functions may be expressed as a linear combination of trigonometric functions using Chebyshev polynomials

[math]\displaystyle{ \cos^n\! \theta = 2^{1-n}\!\mathop{\mathop{{\sum}'}^n_{j=0}}_{n-j\,\mathrm{even}}\!\! \binom{n}{\tfrac{n-j}{2}}\,T_j(\cos \theta), }[/math]

where the prime at the sum symbol indicates that the contribution of j = 0 needs to be halved if it appears, and [math]\displaystyle{ T_j(\cos \theta)=\cos j\theta }[/math].

An important and convenient property of the T_n(x) is that they are orthogonal with respect to the inner product

[math]\displaystyle{ \langle f,g\rangle~=~\int_{-1}^1\,f(x)\,g(x)\,\frac{\mathrm{d}x}{\,\sqrt{1 - x^2\,}\,}~, }[/math]

and U_n(x) are orthogonal with respect to another, analogous inner product product, given below.

This follows from the fact that the Chebyshev polynomials solve the Chebyshev differential equations

[math]\displaystyle{ (1 - x^2)\,y'' - x\,y' + n^2\,y = 0~, }[/math]

[math]\displaystyle{ (1 - x^2)\,y'' - 3\,x\,y' + n\,(n + 2)\,y = 0~, }[/math]

which are Sturm–Liouville differential equations. It is a general feature of such differential equations that there is a distinguished orthonormal set of solutions. (Another way to define the Chebyshev polynomials is as the solutions to those equations.)

The Chebyshev polynomials T_n are polynomials with the largest possible leading coefficient, whose absolute value on the interval [−1, 1] is bounded by 1. They are also the "extremal" polynomials for many other properties.

Chebyshev polynomials are important in approximation theory because the roots of T_n(x), which are also called Chebyshev nodes, are used as matching-points for optimizing polynomial interpolation. The resulting interpolation polynomial minimizes the problem of Runge's phenomenon, and provides an approximation that is close to the best polynomial approximation to a continuous function under the maximum norm, also called the “minimax” criterion. This approximation leads directly to the method of Clenshaw–Curtis quadrature.

These polynomials were named after Pafnuty Chebyshev. The letter T is used because of the alternative transliterations of the name Chebyshev as Tchebycheff, Tchebyshev (French) or Tschebyschow (German).

---