Artificial Neural Network Input Vector
An Artificial Neural Network Input Vector is a Vector that contains all input values that are fed to the artificial neurons in a Neural Network Input Layer.
- AKA: Neuron Input Vector.
- …
- Example(s):
- $\vec{X} = \{x_1, x_2, \cdots , x_m\} $ in the following artificial neuron model:
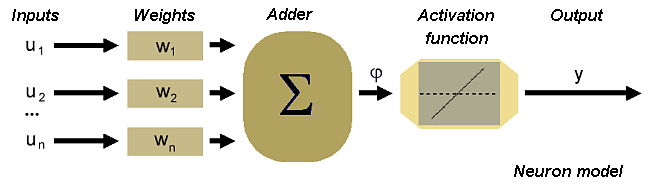
- $\vec{U} = \{u_1, u_2, \cdots , u_n\} $ in the following artificial neuron model:
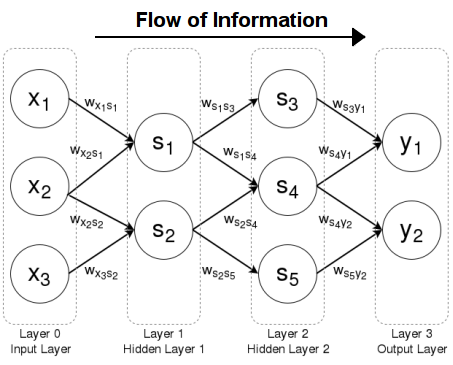
- $\vec{X}=\{x_1,x_2,x_3 \cdots, x_n\}$ in the following Single Layer Neural Network with [math]\displaystyle{ n }[/math] neuron inputs and [math]\displaystyle{ p }[/math] neurons:
- $\vec{X}=\{x_1,x_2, x_3\}$ in the following Feed-Forward Neural Network:
- Counter-Example(s):
- See: Artificial Neural Network, MCP Neuron Model, Artificial Neuron, Fully-Connected Neural Network Layer, Neuron Activation Function, Neural Network Weight, Neural Network Connection, Neural Network Topology, Multi Hidden Layer NNet.
References
2018
- (CS231n, 2018) ⇒ Biological motivation and connections. In: CS231n Convolutional Neural Networks for Visual Recognition Retrieved: 2018-01-14.
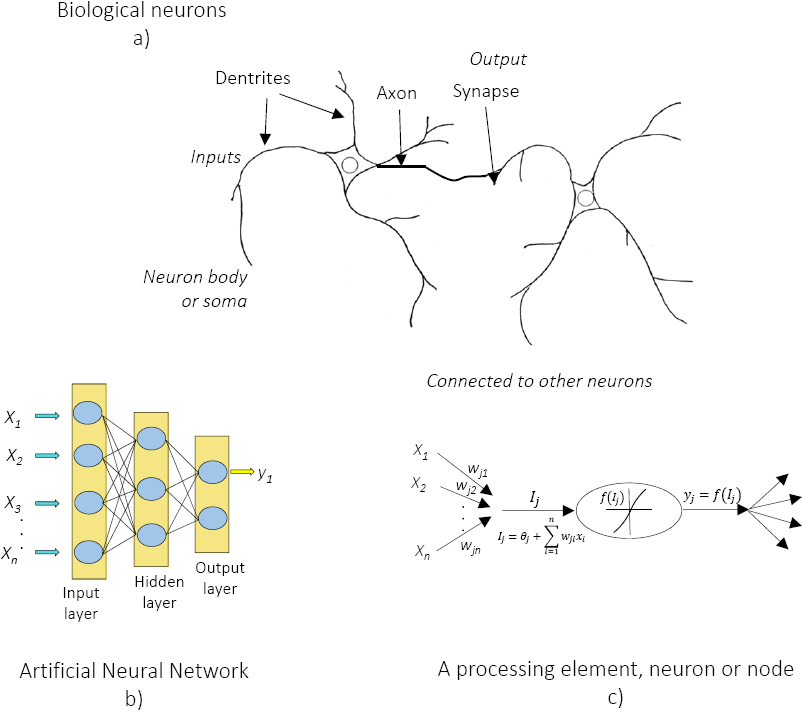
- QUOTE: The diagram below shows a cartoon drawing of a biological neuron (left) and a common mathematical model (right). Each neuron receives input signals from its dendrites and produces output signals along its (single) axon. The axon eventually branches out and connects via synapses to dendrites of other neurons. In the computational model of a neuron, the signals that travel along the axons (e.g. [math]\displaystyle{ x_0 }[/math]) interact multiplicatively (e.g. [math]\displaystyle{ w_0x_0 }[/math]) with the dendrites of the other neuron based on the synaptic strength at that synapse (e.g. [math]\displaystyle{ w_0 }[/math]) (...)
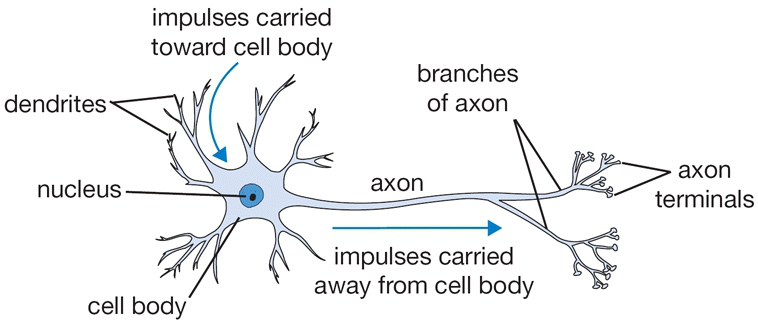
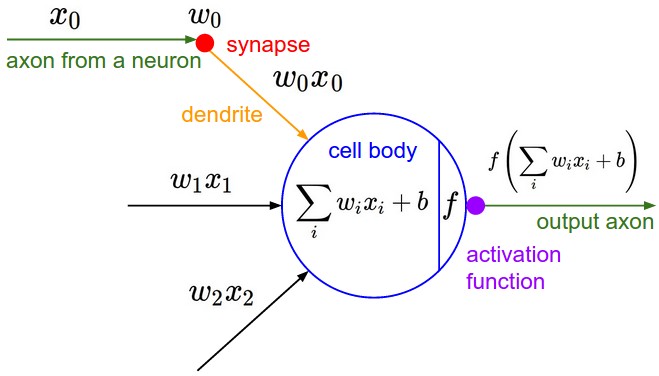
A cartoon drawing of a biological neuron (left) and its mathematical model (right).
- QUOTE: The diagram below shows a cartoon drawing of a biological neuron (left) and a common mathematical model (right). Each neuron receives input signals from its dendrites and produces output signals along its (single) axon. The axon eventually branches out and connects via synapses to dendrites of other neurons. In the computational model of a neuron, the signals that travel along the axons (e.g. [math]\displaystyle{ x_0 }[/math]) interact multiplicatively (e.g. [math]\displaystyle{ w_0x_0 }[/math]) with the dendrites of the other neuron based on the synaptic strength at that synapse (e.g. [math]\displaystyle{ w_0 }[/math]) (...)
2016a
- (Zhao, 2016) ⇒ Peng Zhao, February 13, 2016. R for Deep Learning (I): Build Fully Connected Neural Network from Scratch
- QUOTE: A neuron is a basic unit in the DNN which is biologically inspired model of the human neuron. A single neuron performs weight and input multiplication and addition (FMA), which is as same as the linear regression in data science, and then FMA’s result is passed to the activation function. The commonly used activation functions include sigmoid, ReLu, Tanh and Maxout. In this post, I will take the rectified linear unit (ReLU) as activation function, f(x) = max(0, x). For other types of activation function, you can refer here.

- QUOTE: A neuron is a basic unit in the DNN which is biologically inspired model of the human neuron. A single neuron performs weight and input multiplication and addition (FMA), which is as same as the linear regression in data science, and then FMA’s result is passed to the activation function. The commonly used activation functions include sigmoid, ReLu, Tanh and Maxout. In this post, I will take the rectified linear unit (ReLU) as activation function, f(x) = max(0, x). For other types of activation function, you can refer here.
2016c
- (Garcia et al., 2016) ⇒ García Benítez, S. R., López Molina, J. A., & Castellanos Pedroza, V. (2016). Neural networks for defining spatial variation of rock properties in sparsely instrumented media. Boletín de la Sociedad Geológica Mexicana, 68(3), 553-570.
- QUOTE: The nodes can be seen as computational units that receive external information (inputs) and process it to obtain an answer (output), this processing might be very simple (such as summing the inputs), or quite complex (a node might be another network itself). The connections (weights) determine the information flow between nodes. They can be unidirectional, when the information flows only in one sense, and bidirectional, when the information flows in either sense (...)
- QUOTE: The nodes can be seen as computational units that receive external information (inputs) and process it to obtain an answer (output), this processing might be very simple (such as summing the inputs), or quite complex (a node might be another network itself). The connections (weights) determine the information flow between nodes. They can be unidirectional, when the information flows only in one sense, and bidirectional, when the information flows in either sense (...)
2014
- (Gomes, 2014) ⇒ Lee Gomes (2014). Machine-learning maestro michael jordan on the delusions of big data and other huge engineering efforts. IEEE Spectrum, Oct, 20.
- Michael I. Jordan: … And there, each “neuron” is really a cartoon. It’s a linear-weighted sum that’s passed through a nonlinearity. Anyone in electrical engineering would recognize those kinds of nonlinear systems.
2005
- (Golda, 2005) ⇒ Adam Gołda (2005). Introduction to neural networks. AGH-UST.
- QUOTE: The scheme of the neuron can be made on the basis of the biological cell. Such element consists of several inputs. The input signals are multiplied by the appropriate weights and then summed. The result is recalculated by an activation function.

In accordance with such model, the formula of the activation potential [math]\displaystyle{ \varphi }[/math] is as follows
[math]\displaystyle{ \varphi=\sum_{i=1}^Pu_iw_i }[/math]
Signal [math]\displaystyle{ \varphi }[/math] is processed by activation function, which can take different shapes.
- QUOTE: The scheme of the neuron can be made on the basis of the biological cell. Such element consists of several inputs. The input signals are multiplied by the appropriate weights and then summed. The result is recalculated by an activation function.
2003
- (Aryal & Wang, 2003) ⇒ Aryal, D. R., & Wang, Y. W. (2003). “The Basic Artificial Neuron" In: Neural network Forecasting of the production level of Chinese construction industry. Journal of comparative international management, 6(2).
- QUOTE: The first computational neuron was developed in 1943 by the neurophysiologist Warren McCulloch and the logician Walter Pits based on the biological neuron. It uses the step function to fire when threshold [math]\displaystyle{ \mu }[/math] is exceeded. If the step activation function is used (i.e. the neuron's output is 0 if the input is less than zero, and 1 if the input is greater than or equal to 0) then the neuron acts just like the biological neuron described earlier. Artificial neural networks are comprised of many neurons, interconnected in certain ways to cast them into identifiable topologies as depicted in Figure 2.
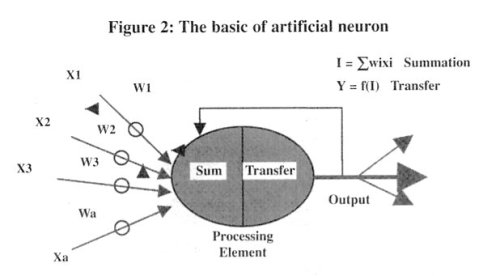
Note that various inputs to the network are represented by the mathematical symbol, [math]\displaystyle{ x(n) }[/math]. Each of these inputs is multiplied by a connection weights [math]\displaystyle{ w(n) }[/math]. In the simplest case, these products are simply summed, fed through a transfer function to generate a result, and then output. Even though all artificial neural networks are constructed from this basic building block the fundamentals vary in these building blocks and there are some differences.
- QUOTE: The first computational neuron was developed in 1943 by the neurophysiologist Warren McCulloch and the logician Walter Pits based on the biological neuron. It uses the step function to fire when threshold [math]\displaystyle{ \mu }[/math] is exceeded. If the step activation function is used (i.e. the neuron's output is 0 if the input is less than zero, and 1 if the input is greater than or equal to 0) then the neuron acts just like the biological neuron described earlier. Artificial neural networks are comprised of many neurons, interconnected in certain ways to cast them into identifiable topologies as depicted in Figure 2.

