Stacked Ensemble-based Learning Algorithm
A Stacked Ensemble-based Learning Algorithm is an ensemble learning algorithm that can be applied by a stacked learning system (that can solve a stacked learning task which creates a decision function which makes its decision based on the outputs of several base models).
- AKA: Stacked Generalization Algorithm, Stacking Algorithm.
- Context:
- It can be implemented by a Stacked Ensemble-based Learning System to solve a Stacked Ensemble-based Learning Task.
- It can range from being Stacked Regression Algorithm to being a Stacked Classification Algorithm.
- It can range from being an Supervised Stacked Generalization Algorithm to being a Unsupervised Stacked Generalization Algorithm.
- Example(s):
- Toscher-Jahrer BigChaos Solution Algorithm - Netflix Grand Prize (Toscher & Jahrer, 2009).
- a GA-Stacking Algorithm (Ledezma et al., 2010),
- a Han-Wilson Dynamic Stacked Generalization Algorithm (Han & Wilson, 2016),
- a Naimi-Balzer Super Learner Stacking Algorithm (Naimi & Balzer, 2018),
- a
sklearn.ensemble.StackingRegressor - a Stacked Auto-Encoding Algorithm,
- a Stacked Decision Tree Algorithm,
- a Stacked Density Estimation Algorithm.
- …
- Counter-Example(s):
- See: Cross-Validation Algorithm, Classification Learning Algorithm, Regression Learning Algorithm, Distance Learning Algorithm, Decision Tree, Estimator, Generalizer, Regressor, Classifier, Additive Model.
References
2020a
- (Wikipedia, 2020) ⇒ https://en.wikipedia.org/wiki/Ensemble_learning#Stacking Retrieved:2020-1-21.
- Stacking (sometimes called stacked generalization) involves training a learning algorithm to combine the predictions of several other learning algorithms. First, all of the other algorithms are trained using the available data, then a combiner algorithm is trained to make a final prediction using all the predictions of the other algorithms as additional inputs. If an arbitrary combiner algorithm is used, then stacking can theoretically represent any of the ensemble techniques described in this article, although, in practice, a logistic regression model is often used as the combiner.
Stacking typically yields performance better than any single one of the trained models. [1] It has been successfully used on both supervised learning tasks (regression, [2] classification and distance learning ) and unsupervised learning (density estimation). [3] It has also been used to estimate bagging's error rate.[4] [5]. It has been reported to out-perform Bayesian model-averaging. [6] The two top-performers in the Netflix competition utilized blending, which may be considered to be a form of stacking.
- Stacking (sometimes called stacked generalization) involves training a learning algorithm to combine the predictions of several other learning algorithms. First, all of the other algorithms are trained using the available data, then a combiner algorithm is trained to make a final prediction using all the predictions of the other algorithms as additional inputs. If an arbitrary combiner algorithm is used, then stacking can theoretically represent any of the ensemble techniques described in this article, although, in practice, a logistic regression model is often used as the combiner.
- ↑ Wolpert, D., Stacked Generalization., Neural Networks, 5(2), pp. 241-259., 1992
- ↑ Breiman, L., Stacked Regression, Machine Learning, 24, 1996
- ↑ Smyth, P. and Wolpert, D. H., Linearly Combining Density Estimators via Stacking, Machine Learning Journal, 36, 59-83, 1999
- ↑ Rokach, L. (2010). “Ensemble-based classifiers". Artificial Intelligence Review. 33 (1–2): 1–39. doi:10.1007/s10462-009-9124-7
- ↑ Wolpert, D.H., and Macready, W.G., An Efficient Method to Estimate Bagging’s Generalization Error, Machine Learning Journal, 35, 41-55, 1999
- ↑ Clarke, B., Bayes model averaging and stacking when model approximation error cannot be ignored, Journal of Machine Learning Research, pp 683-712, 2003
2020b
- (SciKit Learn, 2020) ⇒ https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.StackingRegressor.html Retrieved:2020-1-21.
- QUOTE: Stacked generalization consists in stacking the output of individual estimator and use a regressor to compute the final prediction. Stacking allows to use the strength of each individual estimator by using their output as input of a final estimator.
2018
- (Naimi & Balzer, 2018) ⇒ Ashley I. Naimi, and Laura B. Balzer (2018). "Stacked Generalization: An Introduction to Super Learning". European journal of epidemiology, 33(5), 459-464. DOI: 10.1007/s10654-018-0390-z
- QUOTE: Stacked generalization is an ensemble method that allows researchers to combine several different prediction algorithms into one. Since its introduction in the early 1990s, the method has evolved several times into what is now known as “Super Learner”.
2017
- (Sammut & Webb, 2017) ⇒ Claude Sammut, and Geoffrey I. Webb. (2017). "Stacked Generalization". In: (Sammut & Webb, 2017) p.912
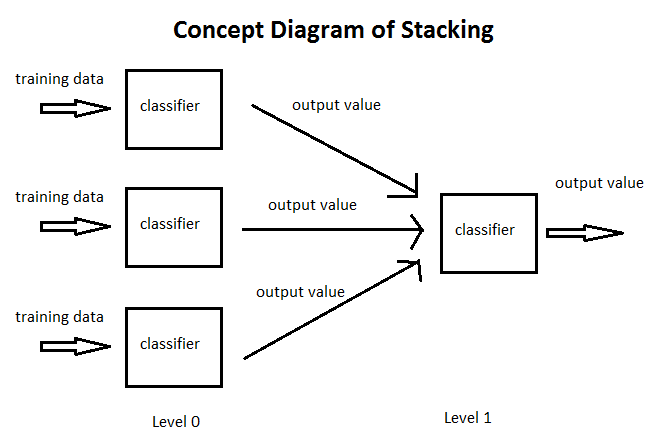
- QUOTE: Stacking is an ensemble learning technique. A set of models are constructed from bootstrap samples of a dataset, then their outputs on a hold-out dataset are used as input to a “meta”-model. The set of base models are called level-0, and the meta-model level-1. The task of the level-1 model is to combine the set of outputs so as to correctly classify the target, thereby correcting any mistakes made by the level-0 models.
2016
- (Han & Wilson, 2016) ⇒ Zhen Han, and Alyson Wilson (2016). "Dynamic Stacked Generalization for Node Classification on Networks". ArXiv:1610.04804.
- QUOTE: Stacked generalization (stacking) [Wolpert, 1992] is a technique for combining multiple classifiers, each of which has been individually trained for a specific classification task, to achieve greater overall predictive accuracy. The method first trains individual classifiers using cross-validation on the training data. The original training data is called level-0 data, and the learned models are called level-0 classifiers. The prediction outcomes from the level-0 models are pooled for the secondstage learning, where a meta-classifier is trained. The pooled classification outcomes are called level-1 data and the metaclassifier is called the level-1 generalizer.
2013
- (LO, 2013) ⇒ http://www.chioka.in/stacking-blending-and-stacked-generalization/ Posted on Sep 5, 2013
- QUOTE: Stacking, Blending and Stacked Generalization are all the same thing with different names. It is a kind of ensemble learning.
In traditional ensemble learning, we have multiple classifiers trying to fit to a training set to approximate the target function. Since each classifier will have its own output, we will need to find a combining mechanism to combine the results. This can be through voting (majority wins), weighted voting (some classifier has more authority than the others), averaging the results, etc. This is the traditional way of ensemble learning.
In stacking, the combining mechanism is that the output of the classifiers (Level 0 classifiers) will be used as training data for another classifier (Level 1 classifier) to approximate the same target function. Basically, you let the Level 1 classifier to figure out the combining mechanism.
- QUOTE: Stacking, Blending and Stacked Generalization are all the same thing with different names. It is a kind of ensemble learning.
2012
- (Domingos, 2012) ⇒ Pedro Domingos. (2012). “A Few Useful Things to Know About Machine Learning.” In: Communications of the ACM Journal, 55(10). doi:10.1145/2347736.2347755
- … In stacking, the outputs of individual classifiers become the inputs of a "higher-level" learner that figures out how best to combine them.
2010
- (Ledezma et al., 2010) ⇒ Agapito Ledezma, Ricardo Aler, Araceli Sanchis, and Daniel Borrajo (2010). "GA-Stacking: Evolutionary Stacked Generalization". Intelligent Data Analysis, 14(1), 89-119.
- QUOTE: Stacking is the abbreviation that refers to Stacked Generalization (Wolpert, 1992). The main idea of Stacking is to combine classifier from different learners such as decision trees, instance-based learners, etc. Since each one uses a different knowledge representation and different learning biases, the hypothesis space will be explored differently, and different classifier will be obtained. Thus, it is expected that their errors will not be perfectly correlated, and that the combination of classifier will perform better than the base classifiers.
2009
- (Toscher & Jahrer, 2009) ⇒ Andreas Toscher, and Michael Jahrer (2009). "The BigChaos Solution To The Netflix Grand Prize". Netflix prize documentation, 1-52.
1999
- (Ting & Witten, 1999) ⇒ K. M. Ting, and I. H. Witten (1999). "Issues in Stacked Generalization". Journal of artificial intelligence research, 10, 271-289.
- QUOTE: Stacked generalization is a way of combining multiple models that have been learned for a classification task (Wolpert, 1992), which has also been used for regression (Breiman, 1996a) and even unsupervised learning (Smyth & Wolpert, 1997). Typically, different learning algorithms learn different models for the task at hand, and in the most common form of stacking the first step is to collect the output of each model into a new set of data. For each instance in the original training set, this data set represents every model's prediction of that instance's class, along with its true classification. During this step, care is taken to ensure that the models are formed from a batch of training data that does not include the instance in question, in just the same way as ordinary cross-validation. The new data are treated as the data for another learning problem, and in the second step a learning algorithm is employed to solve this problem. In Wolpert's terminology, the original data and the models constructed for them in the first step are referred to as level-0 data and level-0 models, respectively, while the set of cross-validated data and the second-stage learning algorithm are referred to as level-1 data and the level-1 generalizer.
1997
- (Smyth & Wolpert, 1997) ⇒ Padhraic Smyth, David H. Wolpert (1997). "Stacked Density Estimation". In: Advances in Neural Information Processing Systems.
- QUOTE: In this paper, the technique of stacking, previously only used for supervised learning, is applied to unsupervised learning. Specifically, it is used for non-parametric multivariate density estimation, to combine finite mixture model and kernel density estimators. Experimental results on both simulated data and real world data sets clearly demonstrate that stacked density estimation outperforms other strategies such as choosing the single best model based on cross-validation, combining with uniform weights, and even the single best model chosen by "cheating" by looking at the data used for independent testing.
1996
- (Breiman, 1996) ⇒ Leo Breiman (1996). "Stacked Regressions". Machine learning, 24(1), 49-64.
- QUOTE: Stacking regressions is a method for forming linear combinations of different predictors to give improved prediction accuracy. The idea is to use cross-validation data and least squares under non-negativity constraints to determine the coefficients in the combination. Its effectiveness is demonstrated in stacking regression trees of different sizes and in a simulation stacking linear subset and ridge regressions. Reasons why this method works are explored. The idea of stacking originated with Wolpert (1992).
1992
- (Wolpert, 1992) ⇒ David H.Wolpert (1992). "Stacked Generalization". Neural networks, 5(2), 241-259. DOI:10.1016/S0893-6080(05)80023-1
- QUOTE: Stacked generalization works by deducing the biases of the generalizer(s) with respect to a provided learning set. This deduction proceeds by generalizing in a second space whose inputs are (for example) the guesses of the original generalizers when taught with part of the learning set and trying to guess the rest of it, and whose output is (for example) the correct guess. When used with multiple generalizers, stacked generalization can be seen as a more sophisticated version of cross-validation, exploiting a strategy more sophisticated than cross-validation's crude winner-takes-all for combining the individual generalizers. When used with a single generalizer, stacked generalization is a scheme for estimating (and then correcting for) the error of a generalizer which has been trained on a particular learning set and then asked a particular question.