Neural Network Pooling Layer
A Neural Network Pooling Layer is a neural network hidden layer that applies a downsampling operation to reduce the spatial dimension of the input data.
- AKA: Down-Sampling Layer.
- Context:
- It can (often) be a part of a Convolutional Neural Network, these are inserted after every convolutional layers.
- Example(s):
- a Max-Pooling Layer,
- an Average-Pooling Layer.
- …
- Counter-Example(s)
- See: Neural Network, Artificial Neuron, Recurrent Neural Network.
References
2018
- (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Convolutional_neural_network#Pooling Retrieved:2018-3-4.
- Convolutional networks may include local or global pooling layers, which combine the outputs of neuron clusters at one layer into a single neuron in the next layer[1][2]. For example, max pooling uses the maximum value from each of a cluster of neurons at the prior layer[3]. Another example is average pooling, which uses the average value from each of a cluster of neurons at the prior layer.
2017a
- (Gibson & Patterson, 2017) ⇒ Adam Gibson, Josh Patterson (2017). "Chapter 4. Major Architectures of Deep Networks". In: "Deep Learning" ISBN: 9781491924570.
- QUOTE: Pooling layers are commonly inserted between successive convolutional layers. We want to follow convolutional layers with pooling layers to progressively reduce the spatial size (width and height) of the data representation. Pooling layers reduce the data representation progressively over the network and help control overfitting. The pooling layer operates independently on every depth slice of the input.
Common Downsampling Operations
The most common downsampling operation is the max operation. The next most common operation is average pooling.
The pooling layer uses the
max()operation to resize the input data spatially (width, height). This operation is referred to as max pooling. With a [math]\displaystyle{ 2 \times 2 }[/math] filter size, themax()operation is taking the largest of four numbers in the filter area. This operation does not affect the depth dimension. Pooling layers use filters to perform the downsampling process on the input volume. These layers perform downsampling operations along the spatial dimension of the input data. This means that if the input image were 32 pixels wide by 32 pixels tall, the output image would be smaller in width and height (e.g., 16 pixels wide by 16 pixels tall). The most common setup for a pooling layer is to apply [math]\displaystyle{ 2 \times 2 }[/math] filters with a stride of 2. This will downsample each depth slice in the input volume by a factor of two on the spatial dimensions (width and height). This downsampling operation will result in 75 percent of the activations being discarded.
Pooling layers do not have parameters for the layer but do have additional hyperparameters. This layer does not involve parameters, because it computes a fixed function of the input volume. It is not common to use zero-padding for pooling layers.
- QUOTE: Pooling layers are commonly inserted between successive convolutional layers. We want to follow convolutional layers with pooling layers to progressively reduce the spatial size (width and height) of the data representation. Pooling layers reduce the data representation progressively over the network and help control overfitting. The pooling layer operates independently on every depth slice of the input.
2017b
- (Rawat & Wang, 2017) ⇒ Rawat, W., & Wang, Z. (2017). Deep convolutional neural networks for image classification: A comprehensive review. Neural computation, 29(9), 2352-2449.
- QUOTE: The purpose of the pooling layers is to reduce the spatial resolution of the feature maps and thus achieve spatial invariance to input distortions and translations (LeCun et al., 1989a, 1989b; LeCun et al., 1998, 2015; Ranzato et al., 2007). Initially, it was common practice to use average pooling aggregation layers to propagate the average of all the input values, of a small neighborhood of an image to the next layer (LeCun et al., 1989a, 1989b; LeCun et al., 1998). However, in more recent models (Ciresan et al., 2011; Krizhevsky et al., 2012; Simonyan & Zisserman, 2014; Zeiler & Fergus, 2014; Szegedy, Liu, et al., 2015; Xu et al., 2015), max pooling aggregation layers propagate the maximum value within a receptive field to the next layer (Ranzato et al., 2007). Formally, max pooling selects the largest element within each receptive field such that
[math]\displaystyle{ Y_{kij}=\underset{(p,q)\in\mathcal{R}_{ij}}{\operatorname{max}} x_{kpq}\quad (2.2) }[/math]
where the output of the pooling operation, associated with the [math]\displaystyle{ k }[/math]th feature map, is denoted by [math]\displaystyle{ Y_{kij},\;x_{kpq} }[/math], denotes the element at location [math]\displaystyle{ (p,q) }[/math] contained by the pooling region [math]\displaystyle{ \mathcal{R}_{ij} }[/math] , which embodies a receptive field around the position [math]\displaystyle{ (i,j) }[/math] (Yu et al., 2014). Figure 2 illustrates the difference between max pooling and average pooling. Given an input image of size 4 4, if a 2 2 filter and stride of two is applied, max pooling outputs the maximum value of each 2 2 region, while average pooling outputs the average rounded integer value of each subsampled region. While the motivations behind the migration toward max pooling are addressed in section 4.2.3, there are also several concerns with max pooling, which have led to the development of other pooling schemes. These are introduced in section 5.1.2.
- QUOTE: The purpose of the pooling layers is to reduce the spatial resolution of the feature maps and thus achieve spatial invariance to input distortions and translations (LeCun et al., 1989a, 1989b; LeCun et al., 1998, 2015; Ranzato et al., 2007). Initially, it was common practice to use average pooling aggregation layers to propagate the average of all the input values, of a small neighborhood of an image to the next layer (LeCun et al., 1989a, 1989b; LeCun et al., 1998). However, in more recent models (Ciresan et al., 2011; Krizhevsky et al., 2012; Simonyan & Zisserman, 2014; Zeiler & Fergus, 2014; Szegedy, Liu, et al., 2015; Xu et al., 2015), max pooling aggregation layers propagate the maximum value within a receptive field to the next layer (Ranzato et al., 2007). Formally, max pooling selects the largest element within each receptive field such that
2016a
- (Cox, 2016) ⇒ Jonathan A. Cox, (2016). https://www.quora.com/What-is-a-downsampling-layer-in-Convolutional-Neural-Network-CNN
- QUOTE: The main type of pooling layer in use today is a "max pooling" layer, where the feature map is downsampled in such a way that the maximum feature response within a given sample size is retained. This is in contrast with average pooling, where you basically just lower the resolution by averaging together a group of pixels. Max pooling tends to do better because it is more responsive to kernels that are "lit up" or respond to patterns detected in the data.
2016b
- (CS231n, 2016) ⇒ http://cs231n.github.io/convolutional-networks/#pool Retrieved: 2016
- QUOTE: It is common to periodically insert a Pooling layer in-between successive Conv layers in a ConvNet architecture. Its function is to progressively reduce the spatial size of the representation to reduce the amount of parameters and computation in the network, and hence to also control overfitting. The Pooling Layer operates independently on every depth slice of the input and resizes it spatially, using the MAX operation. The most common form is a pooling layer with filters of size 2x2 applied with a stride of 2 downsamples every depth slice in the input by 2 along both width and height, discarding 75% of the activations. Every MAX operation would in this case be taking a max over 4 numbers (little 2x2 region in some depth slice). The depth dimension remains unchanged. More generally, the pooling layer:
- Accepts a volume of size W1×H1×D1
- Requires two hyperparameters:
- their spatial extent F,
- the stride S,
- Produces a volume of size W2×H2×D2, where:
- W2=(W1−F)/S+1
- H2=(H1−F)/S+1
- D2=D1
- Introduces zero parameters since it computes a fixed function of the input
- Note that it is not common to use zero-padding for Pooling layers
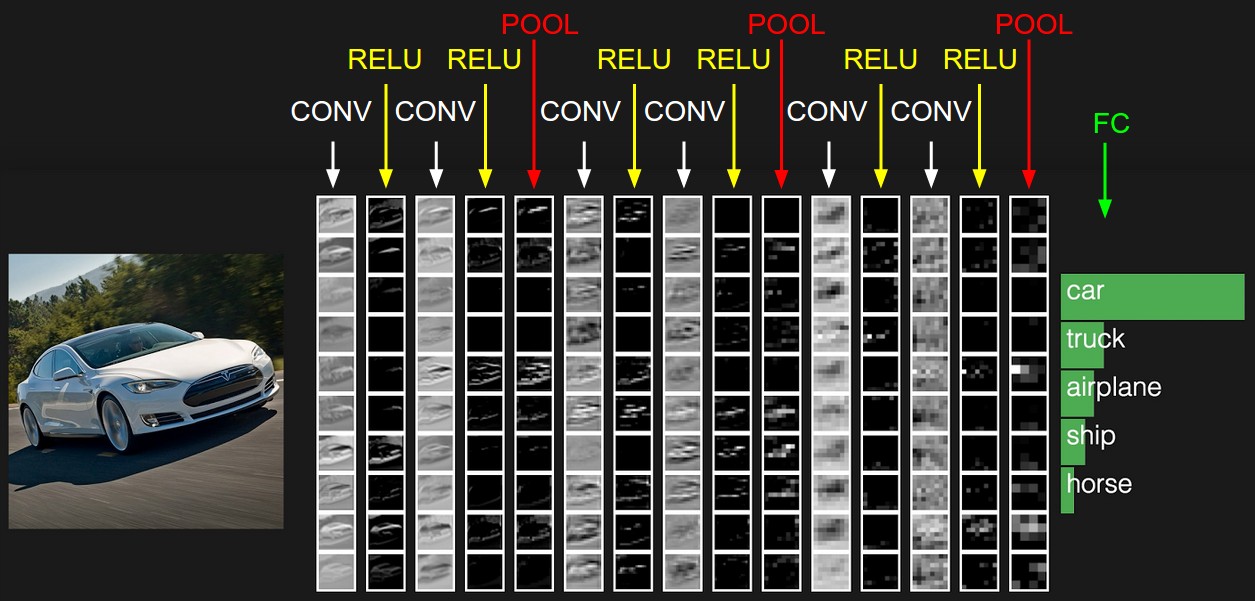
- QUOTE: It is common to periodically insert a Pooling layer in-between successive Conv layers in a ConvNet architecture. Its function is to progressively reduce the spatial size of the representation to reduce the amount of parameters and computation in the network, and hence to also control overfitting. The Pooling Layer operates independently on every depth slice of the input and resizes it spatially, using the MAX operation. The most common form is a pooling layer with filters of size 2x2 applied with a stride of 2 downsamples every depth slice in the input by 2 along both width and height, discarding 75% of the activations. Every MAX operation would in this case be taking a max over 4 numbers (little 2x2 region in some depth slice). The depth dimension remains unchanged. More generally, the pooling layer:
2015
- (Springenberg et al., 2015) ⇒ Jost Tobias Springenberg, Alexey Dosovitskiy, Thomas Brox, and Martin Riedmiller. (2015). “Striving for Simplicity: The All Convolutional Net.” In: ICLR (workshop track).
- QUOTE: Most modern convolutional neural networks (CNNs) used for object recognition are built using the same principles: Alternating convolution and max-pooling layers followed by a small number of fully connected layers. We re-evaluate the state of the art for object recognition from small images with convolutional networks, questioning the necessity of different components in the pipeline. We find that max-pooling can simply be replaced by a convolutional layer with increased stride without loss in accuracy on several image recognition benchmarks.
- ↑ Ciresan, Dan; Ueli Meier; Jonathan Masci; Luca M. Gambardella; Jurgen Schmidhuber (2011). "Flexible, High Performance Convolutional Neural Networks for Image Classification" (PDF). Proceedings of the Twenty-Second international joint conference on Artificial Intelligence-Volume Volume Two. 2: 1237–1242. Retrieved 17 November 2013.
- ↑ Krizhevsky, Alex. "ImageNet Classification with Deep Convolutional Neural Networks" (PDF). Retrieved 17 November 2013.
- ↑ Ciresan, Dan; Meier, Ueli; Schmidhuber, Jürgen (June 2012). "Multi-column deep neural networks for image classification". 2012 IEEE Conference on Computer Vision and Pattern Recognition. New York, NY: Institute of Electrical and Electronics Engineers (IEEE): 3642–3649. arXiv:1202.2745v1 Freely accessible. doi:10.1109/CVPR.2012.6248110. ISBN 978-1-4673-1226-4. OCLC 812295155. Retrieved 2013-12-09.