Universal Turing Machine (UTM)
A Universal Turing Machine (UTM) is a Turing machine that can simulate any other Turing machine.
- Context:
- …
- Counter-Example(s):
- See: Algorithm, Stored Program Computer, Computational Complexity Theory.
References
2020
- https://web.mit.edu/manoli/turing/www/turing.html
- QUOTE: The problem with Turing Machines is that a different one must be constructed for every new computation to be performed, for every input output relation.
This is why we instroduce the notion of a universal turing machine (UTM), which along with the input on the tape, takes in the description of a machine M. The UTM can go on then to simulate M on the rest of the contents of the input tape. A universal turing machine can thus simulate any other machine.
Turing Machine Schematic
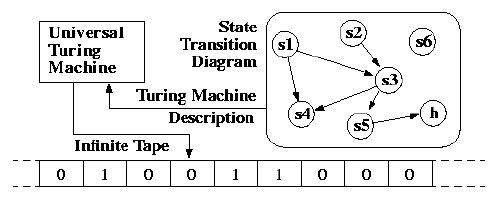
I learned about Turing Machines the first term of my sophomore year at MIT (Fall 96), in 6.004 (Computational Structures), the best class ever conceived. It was late one night when I was starting my problem set on writing a turing machine to compute some operation. To test my result, I figured I could code up a Universal Turing Machine in Scheme to help me do my problem set. I could then feed it my description and a sample input, and it would simulate any machine for me. To my surprise within two hours, the program was working, and i could start the rest of my problem set (You can read on, or simply download the scheme code).
- QUOTE: The problem with Turing Machines is that a different one must be constructed for every new computation to be performed, for every input output relation.
2016
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/Universal_Turing_machine Retrieved:2016-6-2.
- In computer science, a universal Turing machine (UTM) is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan Turing introduced this machine in 1936–1937. This model is considered by some (for example, Martin Davis (2000)) to be the origin of the stored program computer — used by John von Neumann (1946) for the "Electronic Computing Instrument" that now bears von Neumann's name: the von Neumann architecture. It is also known as universal computing machine, universal machine (UM), machine U, U.
In terms of computational complexity, a multi-tape universal Turing machine need only be slower by logarithmic factor compared to the machines it simulates. [1]
- In computer science, a universal Turing machine (UTM) is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan Turing introduced this machine in 1936–1937. This model is considered by some (for example, Martin Davis (2000)) to be the origin of the stored program computer — used by John von Neumann (1946) for the "Electronic Computing Instrument" that now bears von Neumann's name: the von Neumann architecture. It is also known as universal computing machine, universal machine (UM), machine U, U.
- ↑ Arora and Barak, 2009, Theorem 1.9
1936
- (Turing, 1936) ⇒ Alan Mathison Turing. (1936). “On Computable Numbers, with An Application to the Entscheidungsproblem.” In: J. of Math, 58(345-363).