Softplus Activation Function

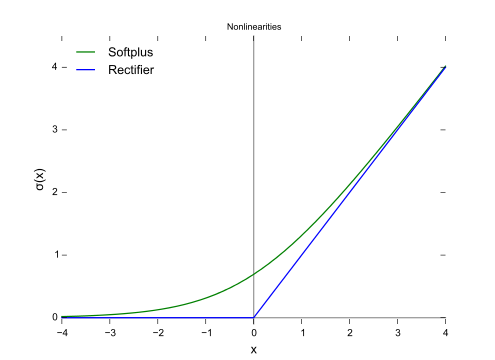
A Softplus Activation Function is a Rectified-based Activation Function that is based on the mathematical function: [math]\displaystyle{ f(x) = \log(1 + \exp x) }[/math].

• Context:
  • It can (typically) be used in the activation of Softplus Neurons.
• Example(s):
  • torch.nn.Softplus
  • chainer.functions.softplus,
  • ...
  • …
• Counter-Example(s):
  • a Clipped Rectifier Unit Activation Function,
  • a Concatenated Rectified Linear Activation Function,
  • an Exponential Linear Activation Function,
  • a Leaky Rectified Linear Activation Function,
  • a Noisy Rectified Linear Activation Function,
  • a Parametric Rectified Linear Activation Function,
  • a Randomized Leaky Rectified Linear Activation Function,
  • a Scaled Exponential Linear Activation Function,
  • a S-shaped Rectified Linear Activation Function,
  • a Soft Shrinkage Activation Function.
• See: Artificial Neural Network, Artificial Neuron, Neural Network Topology, Neural Network Layer, Neural Network Learning Rate.

---

---

References

2018a

• (Pytorch,2018) ⇒ http://pytorch.org/docs/master/nn.html#softplus Retrieved: 2018-2-18.
  • QUOTE: class torch.nn.Softplus(beta=1, threshold=20) source.

    Applies element-wise [math]\displaystyle{ f(x)=\dfrac{1}{beta}∗\log(1+\exp(\beta∗x_i)) }[/math]

     SoftPlus is a smooth approximation to the ReLU function and can be used to constrain the output of a machine to always be positive.

    For numerical stability the implementation reverts to the linear function for inputs above a certain value.

Parameters:

• beta – the beta value for the Softplus formulation. Default: 1
• threshold – values above this revert to a linear function. Default: 20

Shape:

• Input: (N,∗) where * means, any number of additional dimensions
• Output: (N,∗), same shape as the input

Examples:

>>> m = nn.Softplus()
>>> input = autograd.Variable(torch.randn(2))
>>> print(input)
>>> print(m(input)

2018b

• (Chainer, 2018) ⇒ http://docs.chainer.org/en/stable/reference/generated/chainer.functions.softplus.html Retrieved:2018-2-18
  • QUOTE: chainer.functions.softplus(x, beta=1.0)source

    Element-wise softplus function.

    The softplus function is the smooth approximation of ReLU.

    [math]\displaystyle{ f(x)=\dfrac{1}{\beta}\log(1+\exp(\beta x)) }[/math],

    where [math]\displaystyle{ \beta }[/math] is a parameter. The function becomes curved and akin to ReLU as the [math]\displaystyle{ \beta }[/math] is increasing.

Parameters:

• x (Variable or numpy.ndarray or cupy.ndarray) – Input variable. A [math]\displaystyle{ (s_1,s_2,\cdots,s_N) }[/math]-shaped float array.
• beta (float) – Parameter [math]\displaystyle{ \beta }[/math].

Returns: Output variable. A [math]\displaystyle{ (s_1,s_2,\cdots,s_N) }[/math]-shaped float array.

Return type: Variable

Example

>>> x = np.arange(-2, 3, 2).astype('f')
>>> x
array([-2.,  0.,  2.], dtype=float32)
>>> F.softplus(x, beta=1.0).data
array([0.126928 , 0.6931472, 2.126928], dtype=float32)

2018c

• (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Rectifier_(neural_networks) Retrieved:2018-2-4.
  • … A smooth approximation to the rectifier is the analytic function : [math]\displaystyle{ f(x) = \log(1 + \exp x), }[/math] which is called the softplus function. The derivative of softplus is [math]\displaystyle{ f'(x) = \exp x / (1 + \exp x) = 1 / (1 + \exp (-x)) }[/math] , i.e. the logistic function. Rectified linear units find applications in computer vision and speech recognition using deep neural nets.

2017

• (Mate Labs, 2017) ⇒ Mate Labs Aug 23, 2017. Secret Sauce behind the beauty of Deep Learning: Beginners guide to Activation Functions
  • QUOTE: SoftPlus — The derivative of the softplus function is the logistic function. ReLU and Softplus are largely similar, except near 0(zero) where the softplus is enticingly smooth and differentiable. It’s much easier and efficient to compute ReLU and its derivative than for the softplus function which has log(.) and exp(.) in its formulation.

    Range: [math]\displaystyle{ (0, \infty) }[/math]

    Softplus:[math]\displaystyle{ f(x) = \ln(1 + \exp x), }[/math]

    Derivative of the softplus function is the logistic function.

    [math]\displaystyle{ f'(x)=\dfrac{1}{1+e^{-x}} }[/math]

    

---