Single Hidden-Layer Neural Network
A Single Hidden-Layer Neural Network is an artificial neural network composed of one Neural Network Input Layer, one hidden neural network layer and one Neural Network Output Layer.
- AKA: 2-Layer Neural Network.
- Context:
- It can be trained by using a Single Hidden-Layer ANN Training System which implements a Single Hidden-Layer ANN Training Algorithm to solve Single Hidden-Layer ANN Training Task.
- It can (typically) be a Feedforward Neural Network,
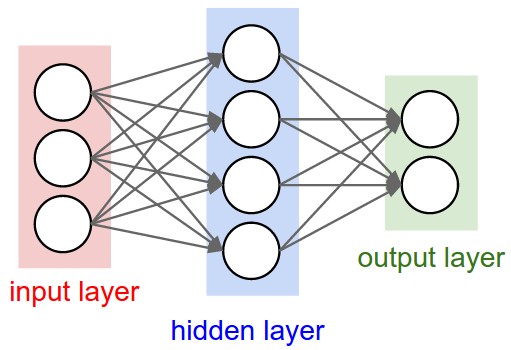
- It can be graphically represented by
where [math]\displaystyle{ \{x_1,\cdots,x_p\} }[/math] is the input vector, [math]\displaystyle{ \{y_1,\cdots,y_m\} }[/math] is the output vector, [math]\displaystyle{ a_j }[/math] is the hidden layer neurons activation, [math]\displaystyle{ w_{ij} }[/math] and [math]\displaystyle{ w_{jk} }[/math] are the input and output weight matrices associated with the synapses or network connections.
- It can be mathematically expressed as
[math]\displaystyle{ y_k=\sum_{j=1}^{n} w_{jk}*a_j+b_2, \quad a_j=f(\sum_{i=1}^{p} w_{ij}*x_i+b_1) }[/math]
where [math]\displaystyle{ \{y_k\}_{k=1}^m }[/math] is the output vector, [math]\displaystyle{ \{a_j\}_{j=1}^n }[/math] is the hidden layer activation, [math]\displaystyle{ f }[/math] is the activation function, [math]\displaystyle{ \{x_i\}_{i=1}^p }[/math] the input vector, [math]\displaystyle{ w_{ij} }[/math] is the input weight matrix,[math]\displaystyle{ \;w_{jk} }[/math] is the output weight matrix, [math]\displaystyle{ b_1 }[/math] is the input layer bias and [math]\displaystyle{ b_2 }[/math] the hidden layer bias.
- Examples(s):
- Counter-Examples(s):
- See: Fully Connected Neural Network, Artificial Neural Network, Neural Network Topology, Single-layer Perceptron, Single-Layer ANN Training System, Activation Function, Artificial Neuron, Neural Network Layer.
References
2017
- (CS231n, 2017) ⇒ http://cs231n.github.io/neural-networks-1/#layers Retrieved: 2017-12-31
- QUOTE: Below are two example Neural Network topologies that use a stack of fully-connected layers:
|
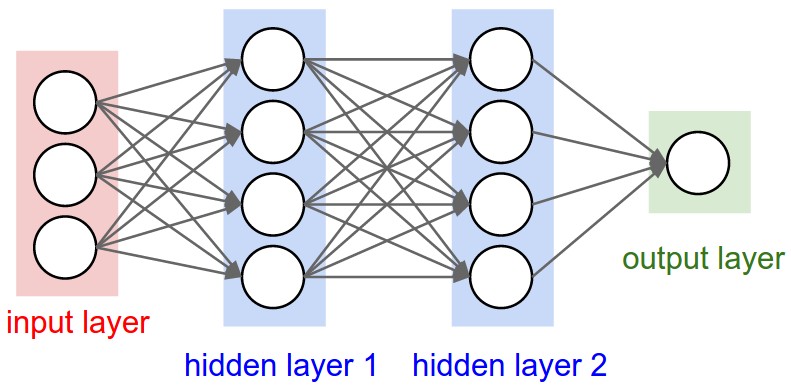
| Left: A 2-layer Neural Network (one hidden layer of 4 neurons (or units) and one output layer with 2 neurons), and three inputs. Right: A 3-layer neural network with three inputs, two hidden layers of 4 neurons each and one output layer. Notice that in both cases there are connections (synapses) between neurons across layers, but not within a layer. |
- Naming conventions. Notice that when we say N-layer neural network, we do not count the input layer. Therefore, a single-layer neural network describes a network with no hidden layers (input directly mapped to output). In that sense, you can sometimes hear people say that logistic regression or SVMs are simply a special case of single-layer Neural Networks. You may also hear these networks interchangeably referred to as “Artificial Neural Networks” (ANN) or “Multi-Layer Perceptrons” (MLP). Many people do not like the analogies between Neural Networks and real brains and prefer to refer to neurons as units.
