Reservoir Computing System
A Reservoir Computing System is a Recurrent Neural Network System in which the input signal is fed into a reservoir and then mapped by readout mechanism to a desired output.
- AKA: Reservoir Computing Neural Network.
- Context
- It can solve a Reservoir Computing Task by implementing a Reservoir Computing Algorithm.
- It can range from being a Single Reservoir Computing System, to being a Dual Reservoir Computing System, to being a Deep Reservoir Computing System.
- Example(s)
- Counter-Example(s)
- See: Dynamical System, Artificial Neural Network, Fully Connected Neural Network Layer, Machine Learning System, Neural Network Training System, Physical Reservoir Computer, Deep Learning System, Extreme Learning Machine, IEEE Task Force on Reservoir Computing.
References
2019a
- (Wikipedia, 2019) ⇒ https://en.wikipedia.org/wiki/Reservoir_computing Retrieved:2019-10-27.
- Reservoir computing is a framework for computation that may be viewed as an extension of neural networks. [1] Typically an input signal is fed into a fixed (random) dynamical system called a reservoir and the dynamics of the reservoir map the input to a higher dimension. Then a simple readout mechanism is trained to read the state of the reservoir and map it to the desired output. The main benefit is that training is performed only at the readout stage and the reservoir is fixed. Liquid-state machines [2] and echo state networks [3] are two major types of reservoir computing. [4] One important feature of this system is that it can use the computational power of naturally available systems which is different from the neural networks and it reduces the computational cost.
2019b
- (TFRC, 2019) ⇒ https://sites.google.com/view/reservoir-computing-tf/home Retrieved:2019-10-27.
- QUOTE: Reservoir Computing is a common denomination for a class of dynamical Recurrent Neural Networks featured by untrained dynamics, including (among the others) Echo State Networks, Liquid State Machines, and Fractal Prediction Machines. As such, Reservoir Computing represents a de facto state-of-the-art paradigm for efficient learning in time series domains.
2019c
- (Tanaka et al., 2019) ⇒ Gouhei Tanaka, Toshiyuki Yamane, Jean Benoit Héroux, Ryosho Nakane, Naoki Kanazawa, Seiji Takeda, Hidetoshi Numata, Daiju Nakano, and Akira Hirose. (2019). “Recent Advances in Physical Reservoir Computing: A Review.” In: Neural Networks - Elsevier Journal, 115. doi:10.1016/j.neunet.2019.03.005
- QUOTE: The architecture of the single-node reservoir with delayed feedback was extended in two ways (Ortín & Pesquera, 2017). One is an ensemble of two separate time-delayed reservoirs whose outputs are combined at the readout. The other is a circular concatenation of the delay lines of two reservoirs, forming a longer delay line. These extended architectures were shown to achieve better performance, faster processing speed, and higher robustness than the single-node reservoir. An extensive amount of work has been performed on single-node reservoirs with delayed feedback (Brunner et al., 2018).

Figure 3. RC using a single nonlinear node reservoir with time-delayed feedback (Appeltant et al., 2011).
2019d
- (Midya et al., 2019) ⇒ Rivu Midya, Zhongrui Wang, Shiva Asapu, Xumeng Zhang, Mingyi Rao, Wenhao Song, Ye Zhuo, Navnidhi Upadhyay, Qiangfei Xia, and J. Joshua Yang. (2019). “Reservoir Computing Using Diffusive Memristors.” In: Advanced Intelligent Systems Journal. doi:10.1002/aisy.201900084
- QUOTE: Initially, reservoir computing (RC) was an RNN‐based framework and hence is suitable for temporal/sequential information processing [4]. RNN models of echo state networks (ESNs) [5] and liquid state machines (LSMs)[6] were proposed independently. These aforementioned models led to the development of the unified computational framework of RC [7]. The backpropagation decorrelation (BPDC) [8] learning is also viewed as a predecessor of RC.
The input data is transformed into spatio-temporal patterns in a high‐dimensional space by an RNN in the reservoir (Figure 1a). Subsequently, the spatio-temporal patterns generated are analyzed for a matching pattern in the readout. The input weights and the weights of the recurrent connections in the reservoir are fixed. The only weights that need to be trained are the weights in the readout layer. This can be done using a simple algorithm‐like linear regression. This offers an inherent advantage, since such simple and fast training reduces the computational cost of learning compared with standard RNNs [9]. RC models have been used for various computational problems such as temporal pattern classification, prediction, and generation. However, to maximize the effectiveness of a certain RC system, it is necessary to appropriately represent sample data and optimize the design of the RNN‐based reservoir [7].
- QUOTE: Initially, reservoir computing (RC) was an RNN‐based framework and hence is suitable for temporal/sequential information processing [4]. RNN models of echo state networks (ESNs) [5] and liquid state machines (LSMs)[6] were proposed independently. These aforementioned models led to the development of the unified computational framework of RC [7]. The backpropagation decorrelation (BPDC) [8] learning is also viewed as a predecessor of RC.

:: Figure 1 Reservoir computing system based on diffusive memristor: a) Schematic of an RC system, showing the reservoir with internal dynamics and a readout function. The weight matrix connecting the reservoir state and the output needs to be trained. b) Equivalent schematic of a simplified system where the reservoir is populated with nodes with recurrent connections having a magnitude less than 1 (...)
2018a
- (Gauthier, 2018) ⇒ Daniel J. Gauthier (March, 2018). "Reservoir Computing: Harnessing a Universal Dynamical System". In: SIAM News.
- QUOTE: Training a “universal” dynamical system to predict the dynamics of a desired system is one approach to this problem that is well-suited for a reservoir computer (RC): a recurrent artificial neural network for processing time-dependent information (see Figure 1 ...)
An RC is distinguished from traditional feed-forward neural networks by the following qualities:
- The network nodes each have distinct dynamical behavior
- Time delays of signals may occur along the network links.
- The network’s hidden part has recurrent connections
- The input and internal weights are fixed and chosen randomly.
- Only the output weights are adjusted during training.
- The last point drastically speeds up the training process.
- QUOTE: Training a “universal” dynamical system to predict the dynamics of a desired system is one approach to this problem that is well-suited for a reservoir computer (RC): a recurrent artificial neural network for processing time-dependent information (see Figure 1 ...)
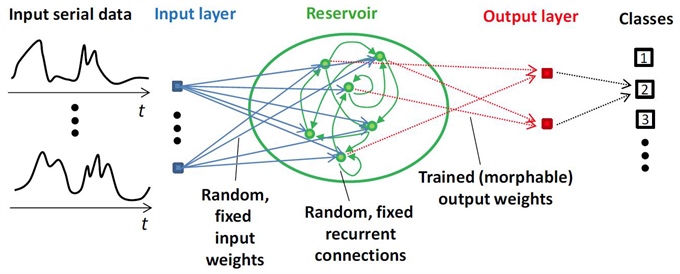
Figure 1. Illustration of the reservoir computer architecture. Figure credit: Daniel J. Gauthier
2018b
- (Krishnagopal et al., 2018) ⇒ Sanjukta Krishnagopal, Yiannis Aloimonos, and Michelle Girvan. (2018). “Generalized Learning with Reservoir Computing.” In: Submitted to Complexity Journal.
- QUOTE: (...) we study the Single Reservoir architecture (Fig. 3(a)). However, there is some evidence that analogy processing involves two steps: 1) the brain generated individual mental representations of the different inputs and 2) brain mapping based on structural similarity, or relationship, between them [29] (...)
- QUOTE: (...) we study the Single Reservoir architecture (Fig. 3(a)). However, there is some evidence that analogy processing involves two steps: 1) the brain generated individual mental representations of the different inputs and 2) brain mapping based on structural similarity, or relationship, between them [29] (...)
- Figure 3: (a) Reservoir architecture with input state of the two images at time [math]\displaystyle{ t }[/math] denoted by [math]\displaystyle{ \vec{u}(t) }[/math], reservoir state at a single time by [math]\displaystyle{ \vec{r}(t) }[/math] and output state by [math]\displaystyle{ \vec{y}(t) }[/math]. (b) shows one image pair from the rotated 90o category of the MNIST dataset split vertically and fed into the reservoir in columns of 1 pixel width, shown to be larger here for ease of visualization.
2017a
- (Miikkulainen, 2017) ⇒ Risto Miikkulainen. (2017). "Reservoir Computing". In: (Sammut & Webb, 2017) DOI:10.1007/978-1-4899-7687-1_731
- QUOTE: Reservoir computing is an approach to sequential processing where recurrency is separated from the output mapping (Jaeger 2003; Maass et al. 2002). The input sequence activates neurons in a recurrent neural network (a reservoir, where activity propagates as in a liquid). The recurrent network is large, nonlinear, randomly connected, and fixed. A linear output network receives activation from the recurrent network and generates the output of the entire machine. The idea is that if the recurrent network is large and complex enough, the desired outputs can likely be learned as linear transformations of its activation. Moreover, because the output transformation is linear, it is fast to train. Reservoir computing has been successful in particular in speech and language processing and vision and cognitive neuroscience.
2017b
- (Du et al., 2017) ⇒ Chao Du, Fuxi Cai, Mohammed A. Zidan, Wen Ma, Seung Hwan Lee, and Wei D. Lu. (2017). “Reservoir Computing Using Dynamic Memristors for Temporal Information Processing.” In: Nature Communications Journal, 8(1). doi:10.1038/s41467-017-02337-y
- QUOTE: Reservoir computing (RC) is a neural network-based computing paradigm that allows effective processing of time varying inputs [1,2,3]. An RC system is conceptually illustrated in Fig. 1a, and can be divided into two parts: the first part, connected to the input, is called the ‘reservoir’. The connectivity structure of the reservoir will remain fixed at all times (thus requiring no training); however, the neurons (network nodes) in the reservoir will evolve dynamically with the temporal input signals(...)
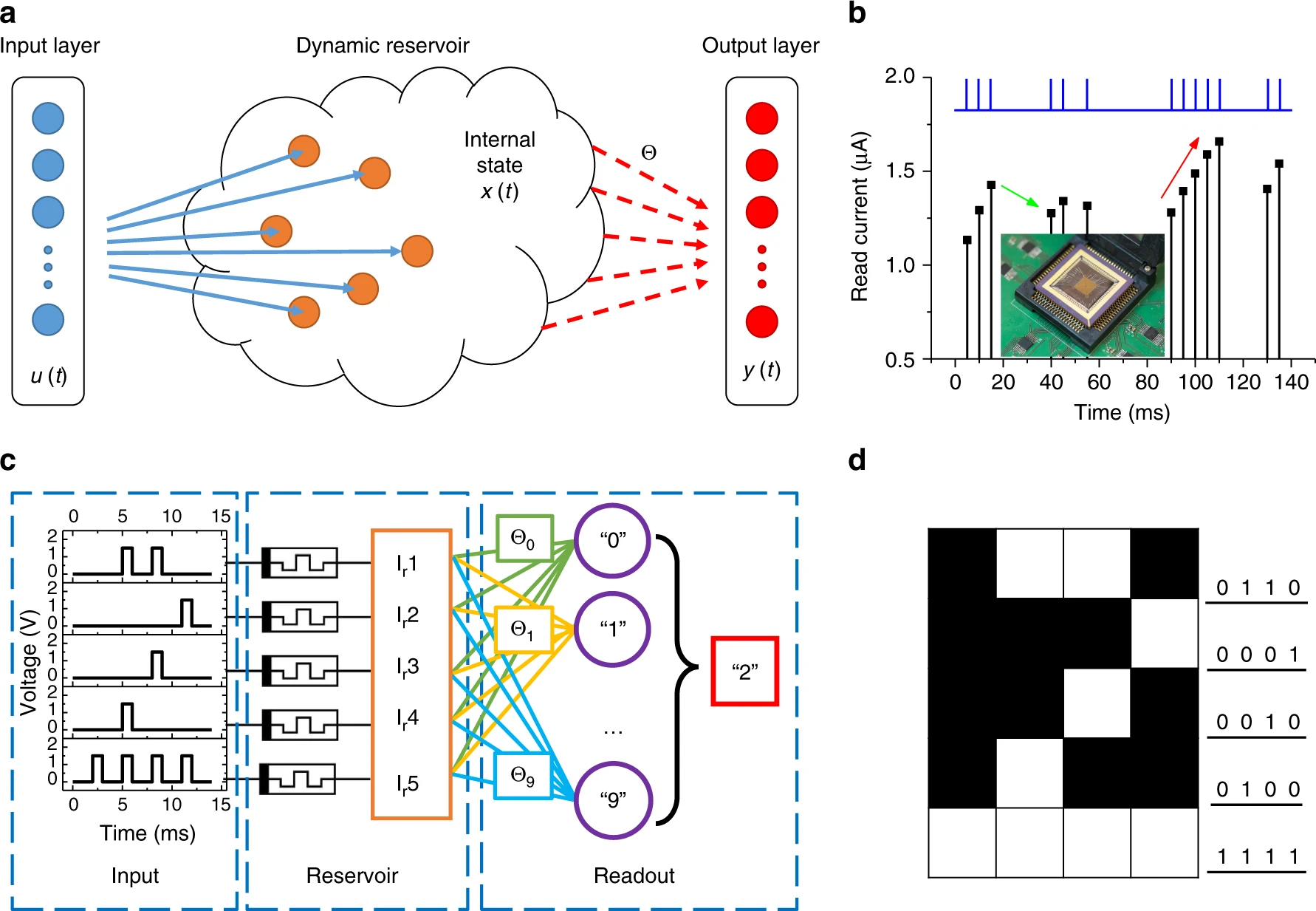
- Figure 1. Reservoir computing system based on a memristor array. a) Schematic of an RC system, showing the reservoir with internal dynamics and a readout function. Only the weight matrix [math]\displaystyle{ \theta }[/math] connecting the reservoir state [math]\displaystyle{ x(t) }[/math] and the output [math]\displaystyle{ y(t) }[/math] needs to be trained. b) Response of a typical WOx memristor to a pulse stream with different time intervals between pulses. Inset: image of the memristor array wired-bonded to a chip carrier and mounted on a test board. c) Schematic of the RC system with pulse streams as the inputs, the memristor reservoir and a readout network. For the simple digit recognition task of 5 × 4 images, the reservoir consists of 5 memristors. d) An example of digit 2 used in the simple digit analysis.
2012
- (Rodan, 2012) ⇒ Ali Rodan. (2012). “Architectural Designs of Echo State Network .” In: Doctoral dissertation, University of Birmingham.
- QUOTE: Reservoir computing (RC) refers to a new class of state-space models with a fixed state transition structure (the “reservoir”) and an adaptable readout from the state space. The reservoir is supposed to be sufficiently complex so as to capture a large number of features of the input stream that can be exploited by the reservoir-to-output readout mapping. The field of RC has been growing rapidly with many successful applications. However, RC has been criticised for not being principled enough. Reservoir construction is largely driven by a series of randomised model building stages, with both researchers and practitioners having to rely on a series of trials and errors. Echo State Networks (ESNs), Liquid State Machines (LSMs) and the back-propagation decorrelation neural network (BPDC) are examples of popular RC methods. In this thesis we concentrate on Echo State Networks, one of the simplest, yet effective forms of reservoir computing.
Echo State Network (ESN) is a recurrent neural network with a non-trainable sparse recurrent part (reservoir) and an adaptable (usually linear) readout from the reservoir. Typically, the reservoir connection weights, as well as the input weights are randomly generated. ESN has been successfully applied in time-series prediction tasks, speech recognition, noise modelling, dynamic pattern classification, reinforcement learning, and in language modelling, and according to the authors, they performed exceptionally well.
- QUOTE: Reservoir computing (RC) refers to a new class of state-space models with a fixed state transition structure (the “reservoir”) and an adaptable readout from the state space. The reservoir is supposed to be sufficiently complex so as to capture a large number of features of the input stream that can be exploited by the reservoir-to-output readout mapping. The field of RC has been growing rapidly with many successful applications. However, RC has been criticised for not being principled enough. Reservoir construction is largely driven by a series of randomised model building stages, with both researchers and practitioners having to rely on a series of trials and errors. Echo State Networks (ESNs), Liquid State Machines (LSMs) and the back-propagation decorrelation neural network (BPDC) are examples of popular RC methods. In this thesis we concentrate on Echo State Networks, one of the simplest, yet effective forms of reservoir computing.
2008
- (Holzmann, 2008) ⇒ Georg Holzmann (2007, 2008). aureservoir - Efficient C++ library for analog reservoir computing neural networks (Echo State Networks).
- QUOTE: Reservoir computing is a recent kind of recurrent neural network computation, where only the output weights are trained. This has the big advantage that training is a simple linear regression task and one cannot get into a local minimum. Such a network consists of a randomly created, fixed, sparse recurrent reservoir and a trainable output layer connected to this reservoir. Most known types are the “Echo State Network” and the “Liquid State Machine", which achieved very promising results on various machine learning benchmarks.
- ↑ Schrauwen, Benjamin, David Verstraeten, and Jan Van Campenhout. “An overview of reservoir computing: theory, applications, and implementations." Proceedings of the European Symposium on Artificial Neural Networks ESANN 2007, pp. 471-482.
- ↑ Mass, Wolfgang, T. Nachtschlaeger, and H. Markram. “Real-time computing without stable states: A new framework for neural computation based on perturbations." Neural Computation 14(11): 2531–2560 (2002).
- ↑ Jaeger, Herbert, "The echo state approach to analyzing and training recurrent neural networks." Technical Report 154 (2001), German National Research Center for Information Technology.
- ↑ Echo state network, Scholarpedia
