Pairwise Correlation Matrix

A Pairwise Correlation Matrix is a Correlation Matrix which elements are pairwise correlation coefficients (i.e. correlation coefficients of pairs of data).

• Example(s):
  • a Pairwise Pearson Correlation Matrix such as:

    

  • a Pairwise Spearman Correlation Matrix,
  • …
• Counter-Example(s)/:
  • Average Pairwise Spearman Correlation,
  • Average Pairwise Pearson Correlation.
• See: Average Pairwise Correlation Coefficient, Pearson Correlation, Spearman Correlation, Covariance, Variance.

---

---

References

2021a

• (Tuychiev, 2021) ⇒ https://towardsdatascience.com/how-to-use-pairwise-correlation-for-robust-feature-selection-20a60ef7d10 Retrieved: 2021-08-01.
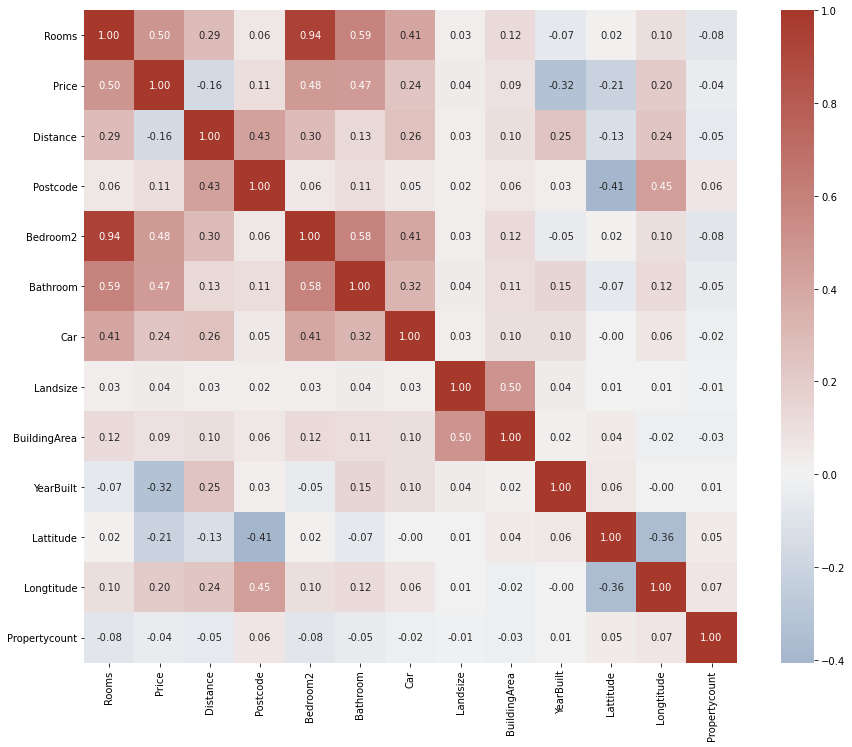
  • QUOTE: The quickest and often the best method of identifying highly correlated features is to use a correlation matrix. This matrix shows the correlation between every single pair of numeric features in the dataset.

    Let’s see one using the Melbourne Housing dataset which contains 13 numeric features:

    (...)

    Calculating the matrix is easily done by calling the .corr() method on the DataFrame. Next, we pass it to Seaborn's heatmap function which is commonly done to generate a nice visual:

    (...)

    

2021b

• (Wetcher-Hendricks, 2021) ⇒ Debra Wetcher-Hendricks (2021). "Correcting the Correction: A Revised Formula to Estimate Partial Correlations between True Scores". In: MDPI Psych, 3(1), 19-24.
  • QUOTE: This formula is one of many commonly used to calculate pairwise correlation coefficients.
    $\rho_{XY}=\dfrac{\sigma_{XY}}{\sigma_X\sigma_Y}$

2018

• (Eslami & Saeed, 2018) ⇒ Taban Eslami, and Fahad Saeed (2018)."Fast-GPU-PCC: A GPU-Based Technique to Compute Pairwise Pearson’s Correlation Coefficients for Time Series Data—fMRI Study". In: MDPI High-throughput, 7(2), 11.
  • QUOTE: Figure 2 shows an example of these elements.

Figure 2: Space needed for computing correlation of first $B$ voxels with the rest of voxels. Pairwise correlation is computed by multiplying a matrix containing time series of $B$ voxels to a matrix containing time series of all voxels which results in a matrix containing $N×\times B$ elements. This matrix has $NB−B(B+1)/2$ distinct correlation coefficients that need to be extracted and stored in the resulting correlation array.

---