Maximum Common Subgraph Task
(Redirected from Maximal Common Subgraph Task)
Jump to navigation
Jump to search
A Maximum Common Subgraph (MCS) Task is a graph matching task that can be solved by a MCS system by implementing a MCS Algorithm.
- AKA: Maximal Common Subgraph Task, Maximum Common Subgraph Isomorphism Task.
- Context:
- It can range from being a Connected Maximum Common Subgraph (cMCS) Task to being a Disconnected Maximum Common Subgraph (dMCS) Task.
- It can range from being an Approximate Maximum Common Subgraph Task being an Exact Maximum Common Subgraph Task.
- Example(s):
- Counter-Example(s)
- See: Maximum Common Induced Subgraph, Maximum common edge subgraph, Common Subgraph Task.
References
2018
- (Duesbury et al., 2018) ⇒ Edmund Duesbury, John Holliday, and Peter Willett. (2018). “Comparison of Maximum Common Subgraph Isomorphism Algorithms for the Alignment of 2D Chemical Structures.” In: ChemMedChem Journal, 13(6). doi:10.1002/cmdc.201700482, PMID: 29057611
- QUOTE: There are two distinct types of MCS. The connected MCS (hereafter cMCS) represents the largest single fragment (in terms of either the number of atoms or the number of bonds) common to two compounds when they are aligned; whereas the disconnected MCS (hereafter dMCS) can contain multiple fragments and is the set of fragments that maximises the number of atoms or bonds in the MCS. The connected and disconnected forms of the MCS are illustrated in Figure 1. There are two additional subdivisions of the MCS: the maximum common edge‐induced subgraph (MCES) representing all the edges (i.e., bonds) between two graphs; and the maximum common node‐induced subgraph (MCIS) representing the nodes (i.e., atoms) in common between two graphs with their respective end‐points preserved.
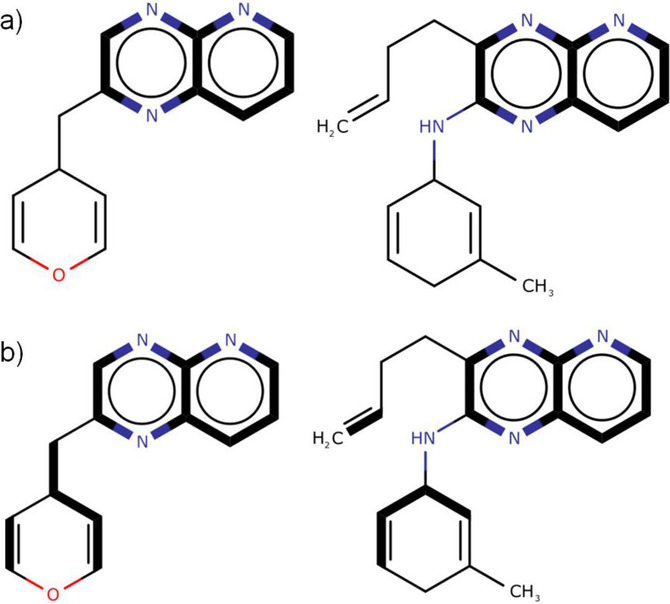
Figure 1. Types of MCES (the MCS in each pair of compounds represented by bold edges): a) cMCS between the two molecular graphs; b) dMCS between the same two molecular graphs.
- QUOTE: There are two distinct types of MCS. The connected MCS (hereafter cMCS) represents the largest single fragment (in terms of either the number of atoms or the number of bonds) common to two compounds when they are aligned; whereas the disconnected MCS (hereafter dMCS) can contain multiple fragments and is the set of fragments that maximises the number of atoms or bonds in the MCS. The connected and disconnected forms of the MCS are illustrated in Figure 1. There are two additional subdivisions of the MCS: the maximum common edge‐induced subgraph (MCES) representing all the edges (i.e., bonds) between two graphs; and the maximum common node‐induced subgraph (MCIS) representing the nodes (i.e., atoms) in common between two graphs with their respective end‐points preserved.
2009
- (Wikipedia, 2009) ⇒ http://en.wikipedia.org/wiki/Maximum_common_subgraph_isomorphism_problem
- In complexity theory, maximum common subgraph-isomorphism (MCS) is an optimization problem that is known to be NP-hard. The formal description of the problem is as follows:
- Maximum common subgraph-isomorphism(G1, G2)
- Input: Two graphs G1 and G2.
- Question: What is the largest induced subgraph of G1 isomorphic to a subgraph of G2?
- The associated decision problem, i.e., given G1, G2 and an integer [math]\displaystyle{ k }[/math], deciding whether G1 contains a subgraph of at least k edges isomorphic to a subgraph of G2 is NP-complete.
- One possible solution for this problem is to build a modular product graph, in which the largest clique represents a solution for the MCS problem.
- MCS algorithms have a long tradition in cheminformatics and pharmacophore mapping.
- In complexity theory, maximum common subgraph-isomorphism (MCS) is an optimization problem that is known to be NP-hard. The formal description of the problem is as follows:
2007
- (Abu-Khzam et al., 2007) ⇒ Faisal N. Abu-Khzam, Nagiza F. Samatova, Mohamad A. Rizk, and Michael A. Langston. (2007). “The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover.” In: Proceedings of 2007 IEEE/ACS International Conference on Computer Systems and Applications. doi:10.1109/AICCSA.2007.370907
- QUOTE: Graph H is said to be common to graphs [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] if both [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] contain induced subgraphs isomorphic to [math]\displaystyle{ H }[/math]. Maximum Common Subgraph (MCS) is usually posed as the following decision problem.
- Inputs: A pair of graphs, [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math], and a positive integer [math]\displaystyle{ k }[/math].
- Question: Do [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ G_2 }[/math] have a common subgraph of order [math]\displaystyle{ k }[/math] or more?
- MCS finds application in many domains. It has been used in bioinformatics [15], chemistry [9, 10], pattern recognition [3, 8], and a variety of other areas. Unfortunately, MCS is an exceedingly difficult problem, with several well-known NP-complete problems reducing to it. The maximum clique problem, for example, corresponds to the special case in which [math]\displaystyle{ |G_1| = |G_2| }[/math] and [math]\displaystyle{ G_1 }[/math] is complete.
2004
- (Yamaguchi, et al., 2004) ⇒ Atsuko Yamaguchi, Kiyoko F.Aoki and Hiroshi Mamitsuka (2004). "Finding the maximum common subgraph of a partial k-tree and a graph with a polynomially bounded number of spanning trees". Information Processing Letters, 92(2), 57-63.
2003
- (Massaro & Pelillo, 2003) ⇒ Alessio Massaro, and Marcello Pelillo. (2003). “Matching Graphs by Pivoting.” In: Pattern Recognition Letters Journal, 24(8). doi:10.1016/S0167-8655(02)00256-8
2002a
- (Raymond & Willett, 2002) ⇒ John W. Raymond, and Peter Willett. (2002). “Maximum Common Subgraph Isomorphism Algorithms for the Matching of Chemical Structures.” In: Journal of Computer-Aided Molecular Design, 16. doi:https://doi.org/10.1023/A:1021271615909
- QUOTE: Due to this complexity problem and the inherent usefulness of the MCS problem, there have been many attempts to devise usable MCS algorithms. A natural classification criterion for these algorithms is whether the algorithm is intended as an approximation of the MCS or whether it results in the exact determination of the MCS for a specialized set of graphs or graphs of moderate size. As mentioned previously, these two classifications can be further divided into those algorithms which are restricted to the case of the connected MCS or are capable of calculating a potentially disconnected MCS (see Figure 4).

Figure 4. MCS algorithm classification.
- QUOTE: Due to this complexity problem and the inherent usefulness of the MCS problem, there have been many attempts to devise usable MCS algorithms. A natural classification criterion for these algorithms is whether the algorithm is intended as an approximation of the MCS or whether it results in the exact determination of the MCS for a specialized set of graphs or graphs of moderate size. As mentioned previously, these two classifications can be further divided into those algorithms which are restricted to the case of the connected MCS or are capable of calculating a potentially disconnected MCS (see Figure 4).
2002b
- (Bunke et al., 2002) ⇒ Horst Bunke, Pasquale Foggia, Corrado Guidobaldi, Carlo Sansone, and Mario Vento. (2002). “A Comparison of Algorithms for Maximum Common Subgraph on Randomly Connected Graphs.” In: Proceedings of the Joint IAPR International Workshop on Structural, Syntactic, and Statistical Pattern Recognition. ISBN:ISBN:3-540-44011-9 doi:https://doi.org/10.1007/3-540-70659-3_12
1998
- (Bunke & Shearer, 1998) ⇒ Horst Bunke, and Kim Shearer. (1998). “A Graph Distance Metric Based on the Maximal Common Subgraph.” In: Pattern Recognition Letters, 19(3-4).
- Defines Maximum Common Subgraph Task
1997
- (Bunke, 1997) ⇒ Horst Bunke. (1997). “On a Relation Between Graph Edit Distance and Maximum Common Subgraph.” In: Pattern Recognition Letters, 18(9).
- ABSTRACT: In approximate, or error-correcting, graph matching one considers a set of graph edit operations, and defines the edit distance of two graphs g1 and g2 as the shortest (or least cost) sequence of edit operations that transform g1 into g2. A maximum common subgraph of two graphs g1 and g2 is a subgraph of both g1 and g2 such that there is no other subgraph of g1 and g2 with more nodes. Graph edit distance and maximum common subgraph are well known concepts that have various applications in pattern recognition and machine vision. In this paper a particular cost function for graph edit distance is introduced, and it is shown that under this cost function graph edit distance computation is equivalent to the maximum common subgraph problem.
1992
- (Kann, 1992) ⇒ Viggo Kann. (1992). “On the Approximability of the Maximum Common Subgraph Problem.” In: Proceedings of the 9th Annual Symposium on Theoretical Aspects of Computer Science (STACS 92). ISBN:978-3-540-46775-5 doi:10.1007/3-540-55210-3_198
1981
- (McGregor & Willett, 1981) ⇒ James J. McGregor, and Peter Willett (1981). "Use of a maximum common subgraph algorithm in the automatic identification of ostensible bond changes occurring in chemical reactions". Journal of Chemical Information and Computer Sciences, 21(3), 137-140.