Legendre Polynomial
(Redirected from Legendre function)
Jump to navigation
Jump to search
A Legendre Polynomial is an orthogonal polynomial that is a solution to the Legendre differential equation.
- AKA: Legendre Functions of the First Kind, Legendre Coefficients, Zonal Harmonics.
- Example(s):
- $P_0(x) = 1$
- $P_1(x) = x$
- $P_2(x) = \dfrac{1}{2}(3x^2-1)$
- $P_3(x) = \dfrac{1}{2}(5x^3-3x)$
- $P_4(x) = \dfrac{1}{8}(35x^4-30x^2+3)$
- Counter-Example(s):
- See: Associated Legendre Function, Mathematics, Adrien-Marie Legendre, Orthogonal Polynomial, Associated Legendre Polynomials, Legendre Function.
References
2021a
- (Wikipedia, 2021) ⇒ https://en.wikipedia.org/wiki/Legendre_polynomials Retrieved:2021-9-12.
- In physical science and mathematics, Legendre polynomials (named after Adrien-Marie Legendre, who discovered them in 1782) are a system of complete and orthogonal polynomials, with a vast number of mathematical properties, and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications.
Closely related to the Legendre polynomials are associated Legendre polynomials, Legendre functions, Legendre functions of the second kind, and associated Legendre functions.
- In physical science and mathematics, Legendre polynomials (named after Adrien-Marie Legendre, who discovered them in 1782) are a system of complete and orthogonal polynomials, with a vast number of mathematical properties, and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications.
2021b
- (MathWolfram, 2021) ⇒ https://mathworld.wolfram.com/LegendrePolynomial.html Retrieved:2021-9-12.
- QUOTE: The Legendre polynomials, sometimes called Legendre functions of the first kind, Legendre coefficients, or zonal harmonics (Whittaker and Watson 1990, p. 302), are solutions to the Legendre differential equation. If $l$ is an integer, they are polynomials. The Legendre polynomials $P_n(x)$ are illustrated above for $x$ in $[-1,1]$ and $n=1, 2, ..., 5$. They are implemented in the Wolfram Language as LegendreP[n, x].
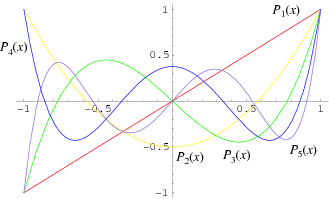
- QUOTE: The Legendre polynomials, sometimes called Legendre functions of the first kind, Legendre coefficients, or zonal harmonics (Whittaker and Watson 1990, p. 302), are solutions to the Legendre differential equation. If $l$ is an integer, they are polynomials. The Legendre polynomials $P_n(x)$ are illustrated above for $x$ in $[-1,1]$ and $n=1, 2, ..., 5$. They are implemented in the Wolfram Language as LegendreP[n, x].