Gradient Clipping Algorithm
Jump to navigation
Jump to search
A Gradient Clipping Algorithm is a Neural Network Training Algorithm that used to solve exploding and vanishing gradient problem.
- Example(s):
- Counter-Example(s):
- See: Recurrent Neural Network, Residual Network, Rectified Linear Unit, Backpropagation, Gradient Descent Algorithm.
References
2021a
- (Shervine, 2021) ⇒ https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks#architecture Retrieved:2021-07-04.
- QUOTE: Gradient clipping - It is a technique used to cope with the exploding gradient problem sometimes encountered when performing backpropagation. By capping the maximum value for the gradient, this phenomenon is controlled in practice.
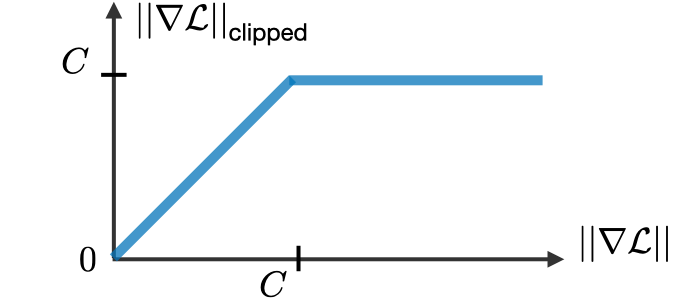
- QUOTE: Gradient clipping - It is a technique used to cope with the exploding gradient problem sometimes encountered when performing backpropagation. By capping the maximum value for the gradient, this phenomenon is controlled in practice.
2021b
- (Deep-AI, 2021) ⇒ https://deepai.org/machine-learning-glossary-and-terms/gradient-clipping Retrieved:2021-07-04.
- QUOTE: Gradient clipping is a technique to prevent exploding gradients in very deep networks, usually in recurrent neural networks. A neural network is a learning algorithm, also called neural network or neural net, that uses a network of functions to understand and translate data input into a specific output. This type of learning algorithm is designed based on the way neurons function in the human brain. There are many ways to compute gradient clipping, but a common one is to rescale gradients so that their norm is at most a particular value. With gradient clipping, pre-determined gradient threshold be introduced, and then gradients norms that exceed this threshold are scaled down to match the norm. This prevents any gradient to have norm greater than the threshold and thus the gradients are clipped. There is an introduced bias in the resulting values from the gradient, but gradient clipping can keep things stable.
2021c
- (Mai & Johansson, 2021) ⇒ Vien V. Mai, and Mikael Johansson (2021). "Stability and Convergence of Stochastic Gradient Clipping: Beyond Lipschitz Continuity and Smoothness". In: arXiv:2102.06489.
- QUOTE: Gradient clipping is a simple and effective technique to stabilize the training process for problems that are prone to the exploding gradient problem. Despite its widespread popularity, the convergence properties of the gradient clipping heuristic are poorly understood, especially for stochastic problems. This paper establishes both qualitative and quantitative convergence results of the clipped stochastic (sub)gradient method (SGD) for non-smooth convex functions with rapidly growing subgradients.
2020
- (Zhang et al., 2020) ⇒ Jingzhao Zhang, Tianxing He, aSuvrit Sra, and Ali Jadbabaie. (2020). “Why Gradient Clipping Accelerates Training: A Theoretical Justification for Adaptivity.” In: Proceedings of the 8th International Conference on Learning Representations (ICLR 2020).