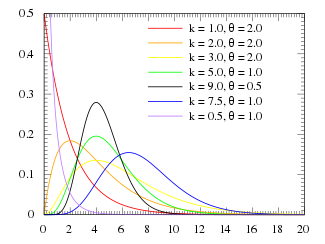
Gamma Density Function
(Redirected from Gamma Probability Function)
Jump to navigation
Jump to search
A Gamma Density Function is a probability density function from a gamma distribution family.
- …
- Example(s):
- [math]\displaystyle{ \gamma(k=7.5, \theta=0.5) }[/math].
- a Chi-Square Function.
- …
- Counter-Example(s):
- See: Binomial Density Function, Shape Parameter.
References
2006
- (Dubnicka, 2006g) ⇒ Suzanne R. Dubnicka. (2006). “Special Continuous Distributions - Handout 7." Kansas State University, Introduction to Probability and Statistics I, STAT 510 - Fall 2006.
- THE GAMMA FUNCTION: The gamma function is a function of t, defined for all k > 0 as ...
- TERMINOLOGY : A random variable X is said to have a gamma distribution with parameters k > 0 and > 0 if its pdf is given by fX(x) =
- …
- 0, otherwise.
- TERMINOLOGY : In the Gamma(k, ) family, when k = /2, for any integer , and = 1/2, we call the resulting distribution a 2 distribution with degrees of freedom. If X has a 2 distribution with degrees of freedom, we write X ∼ 2().