Feed-Forward Neural Network
A Feed-Forward Neural Network is an artificial neural network that follows a feed-forward neural architecture (mapped to a directed acyclic graph).
- AKA: FF, FFANN, FFNN, FFN.
- Context:
- It can range from being a Single-layer Perceptron to being a Multilayer Feedforward Network.
- It can be trained by a Feed-Forward Neural Network Training System (that implements a feed-forward neural network training algorithm).
- It can range from being Shallow Feedforward Neural Network to being a Deep Feedforward Neural Network.
- …
- Example(s):
- Counter-Example(s):
- See: Directed Cycle, Backprop Algorithm, Perceptron Model.
References
2018
- (Brilliant, 2018) ⇒ https://brilliant.org/wiki/feedforward-neural-networks/ Retrieved:2018-9-2.
- QUOTE: Feedforward Neural Networks are artificial neural networks where the connections between units do not form a cycle. Feedforward neural networks were the first type of artificial neural network invented and are simpler than their counterpart, recurrent neural networks. They are called feedforward because information only travels forward in the network (no loops), first through the input nodes, then through the hidden nodes (if present), and finally through the output nodes.
Feedfoward neural networks are primarily used for supervised learning in cases where the data to be learned is neither sequential nor time-dependent. That is, feedforward neural networks compute a function [math]\displaystyle{ f }[/math] on fixed size input [math]\displaystyle{ x }[/math] such that [math]\displaystyle{ f(x) \approx y }[/math] for training pairs [math]\displaystyle{ (x, y) }[/math]. On the other hand, recurrent neural networks learn sequential data, computing [math]\displaystyle{ g }[/math] on variable length input [math]\displaystyle{ X_k = \{x_1, \dots, x_k\} }[/math] such that [math]\displaystyle{ g(X_k) \approx y_k }[/math] for training pairs [math]\displaystyle{ (X_n, Y_n) }[/math] for all [math]\displaystyle{ 1 \le k \le n }[/math].
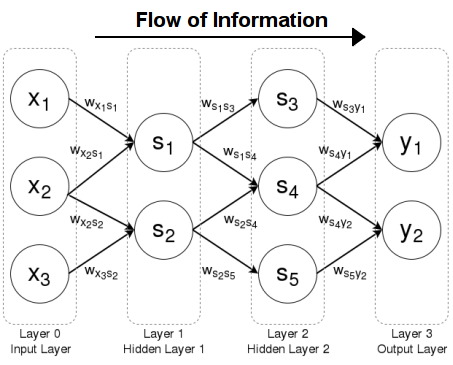
A feedforward neural network with information flowing left to right
- QUOTE: Feedforward Neural Networks are artificial neural networks where the connections between units do not form a cycle. Feedforward neural networks were the first type of artificial neural network invented and are simpler than their counterpart, recurrent neural networks. They are called feedforward because information only travels forward in the network (no loops), first through the input nodes, then through the hidden nodes (if present), and finally through the output nodes.
2017
- (Munro,2017) ⇒ Munro P. (2017) "Backpropagation". In: Sammut, C., Webb, G.I. (eds) "Encyclopedia of Machine Learning and Data Mining". Springer, Boston, MA
- QUOTE: A feed-forward neural network is a mathematical function that is composed of constituent “semi-linear” functions constrained by a feed-forward network architecture, wherein the constituent functions correspond to nodes (often called units or artificial neurons) in a graph, as in Fig. 1. A feed-forward network architecture has a connectivity structure that is an acyclic graph; that is, there are no closed loops.
2015
- (Schmidhuber, 2015) ⇒ Jurgen Schmidhuber (2015). "Deep learning in neural networks: An overview". Neural networks, 61, 85-117. DOI: 10.1016/j.neunet.2014.09.003 arxiv: 1404.7828
- QUOTE: FNNs are acyclic graphs, RNNs cyclic. The first (input) layer is the set of input units, a subset of [math]\displaystyle{ N }[/math]. In FNNs, the k-th layer ([math]\displaystyle{ k \gt 1 }[/math]) is the set of all nodes [math]\displaystyle{ u \in N }[/math] such that there is an edge path of length [math]\displaystyle{ k − 1 }[/math] (but no longer path) between some input unit and [math]\displaystyle{ u }[/math]. There may be shortcut connections between distant layers.
2012
- (Wilson, 2012) ⇒ Bill Wilson (2012). "feedforward net". In: The Machine Learning Dictionary for COMP9414
- QUOTE: A kind of neural network in which the nodes can be numbered, in such a way that each node has weighted connections only to nodes with higher numbers. Such nets can be trained using the error backpropagation learning algorithm.
In practice, the nodes of most feedforward nets are partitioned into layers - that is, sets of nodes, and the layers may be numbered in such a way that the nodes in each layer are connected only to nodes in the next layer - that is, the layer with the next higher number. Commonly successive layers are totally interconnected - each node in the earlier layer is connected to every node in the next layer.
The first layer has no input connections, so consists of input units and is termed the input layer (yellow nodes in the diagram below).
The last layer has no output connections, so consists of output units and is termed the output layer (maroon nodes in the diagram below).
The layers in between the input and output layers are termed hidden layers, and consist of hidden units (light blue nodes and brown nodes in the diagram below).
When the net is operating, the activations of non-input neurons are computing using each neuron's activation function.

Feedforward network. All connections (arrows) are in one direction; there are no cycles of activation flow (cyclic subgraphs). Each colour identifies a different layer in the network. The layers 1 and 2 are fully interconnected, and so are layers 3 and 4. Layers 2 and 3 are only partly interconnected.
- QUOTE: A kind of neural network in which the nodes can be numbered, in such a way that each node has weighted connections only to nodes with higher numbers. Such nets can be trained using the error backpropagation learning algorithm.
2005
- (Golda, 2005) ⇒ Adam Golda (2005). "Introduction to neural networks"
- QUOTE: Feedforward neural networks, which typical example is one-layer perceptron (see figure of Single-layer perceptron), consist of neurons set in layers. The information flow has one direction. Neurons from a layer are connected only with the neurons from the preceding layer. The multi-layer networks usually consist of input, hidden (one or more), and output layers. Such system may be treated as non-linear function approximation block: [math]\displaystyle{ y = f(u) }[/math].
1994
- (Zell, 1994) ⇒ Andreas Zell (1994). Simulation Neuronaler Netze [Simulation of Neural Networks] (in German) (1st ed.). Addison-Wesley. p. 73. ISBN 3-89319-554-8.