Cyclical Learning Rate (CLR)
Jump to navigation
Jump to search
A Cyclical Learning Rate (CLR) is a learning rate that varies cyclically between a minimum and a maximum bound.
- Example(s):
- Counter-Example(s):
- See: Convex Optimization, Gradient Descent, Proximal Function, Hebb's Rule, Loss Function, Neural Network Topology, Stochastic Gradient Descent, Adam, Backprop.
References
2018
- (Apache Incubator, 2018) ⇒ https://mxnet.incubator.apache.org/tutorials/gluon/learning_rate_schedules_advanced.html Retrieved: 2018-10-20.
- QUOTE: Originally proposed by Leslie N. Smith (2015), the idea of cyclically increasing and decreasing the learning rate has been shown to give faster convergence and more optimal solutions. We implement a wrapper class that loops existing cycle-based schedules such as
TriangularScheduleandCosineAnnealingScheduleto provide infinitely repeating schedules (...)schedule = CyclicalSchedule(TriangularSchedule, min_lr=0.5, max_lr=2, cycle_length=500)plot_schedule(schedule)
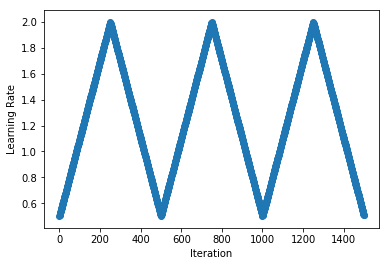
- QUOTE: Originally proposed by Leslie N. Smith (2015), the idea of cyclically increasing and decreasing the learning rate has been shown to give faster convergence and more optimal solutions. We implement a wrapper class that loops existing cycle-based schedules such as
- (...)schedule = CyclicalSchedule(CosineAnnealingSchedule, min_lr=0.01, max_lr=2, cycle_length=250, cycle_length_decay=2, cycle_magnitude_decay=0.5)
plot_schedule(schedule)

- (...)
2017a
- (Smith, 2017) ⇒ Leslie N. Smith (2017, March). "Cyclical learning rates for training neural networks" (PDF). In Applications of Computer Vision (WACV), 2017 IEEE Winter Conference on (pp. 464-472). IEEE. arXiv:1506.01186
- QUOTE: The essence of this learning rate policy comes from the observation that increasing the learning rate might have a short term negative effect and yet achieve a longer term beneficial effect. This observation leads to the idea of letting the learning rate vary within a range of values rather than adopting a stepwise fixed or exponentially decreasing value. That is, one sets minimum and maximum boundaries and the learning rate cyclically varies between these bounds. Experiments with numerous functional forms, such as a triangular window (linear), a Welch window (parabolic) and a Hann window (sinusoidal) all produced equivalent results This led to adopting a triangular window (linearly increasing then linearly decreasing), which is illustrated in Figure 2, because it is the simplest function that incorporates this idea.
Figure 2. Triangular learning rate policy. The blue lines represent learning rate values changing between bounds. The input parameter stepsize is the number of iterations in half a cycle.
- QUOTE: The essence of this learning rate policy comes from the observation that increasing the learning rate might have a short term negative effect and yet achieve a longer term beneficial effect. This observation leads to the idea of letting the learning rate vary within a range of values rather than adopting a stepwise fixed or exponentially decreasing value. That is, one sets minimum and maximum boundaries and the learning rate cyclically varies between these bounds. Experiments with numerous functional forms, such as a triangular window (linear), a Welch window (parabolic) and a Hann window (sinusoidal) all produced equivalent results This led to adopting a triangular window (linearly increasing then linearly decreasing), which is illustrated in Figure 2, because it is the simplest function that incorporates this idea.
2017b
- (Smith & Topin, 2017) ⇒ Leslie N. Smith, and Nicholay Topin (2017). "Super-Convergence: Very Fast Training of Residual Networks Using Large Learning Rates". arXiv preprint arXiv:1708.07120.
- QUOTE: While deep neural networks have achieved amazing successes in a range of applications, understanding why stochastic gradient descent (SGD) works so well remains an open and active area of research. Specifically, we show that, for certain hyper-parameter values, using very large learning rates with the cyclical learning rate (CLR) method [Smith, 2015, 2017] can speed up training by as much as an order of magnitude. We named this phenomenon “super-convergence.” In addition to the practical value of super-convergence training, this paper provides empirical support and theoretical insights to the active discussions in the literature on stochastic gradient descent (SGD) and understanding generalization.
