Variational Autoencoding (VAE) Algorithm
Jump to navigation
Jump to search
A Variational Autoencoding (VAE) Algorithm is an autoencoding algorithm that ...
- See: Denoising Autoencoder.
References
2018
- https://towardsdatascience.com/intuitively-understanding-variational-autoencoders-1bfe67eb5daf
- QUOTE: ... Variational Autoencoders (VAEs) have one fundamentally unique property that separates them from vanilla autoencoders, and it is this property that makes them so useful for generative modeling: their latent spaces are, by design, continuous, allowing easy random sampling and interpolation. ...
...
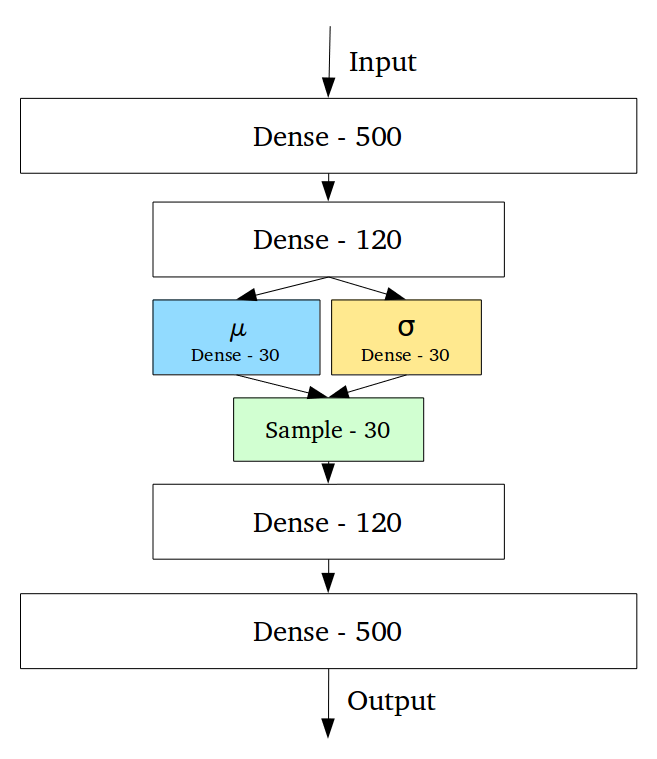
- QUOTE: ... Variational Autoencoders (VAEs) have one fundamentally unique property that separates them from vanilla autoencoders, and it is this property that makes them so useful for generative modeling: their latent spaces are, by design, continuous, allowing easy random sampling and interpolation. ...
2016
- (Doersch, 2016) ⇒ Carl Doersch. (2016). “Tutorial on Variational Autoencoders.” arXiv preprint arXiv:1606.05908
- ABSTRACT: In just three years, Variational Autoencoders (VAEs) have emerged as one of the most popular approaches to unsupervised learning of complicated distributions. VAEs are appealing because they are built on top of standard function approximators (neural networks), and can be trained with stochastic gradient descent. VAEs have already shown promise in generating many kinds of complicated data, including handwritten digits, faces, house numbers, CIFAR images, physical models of scenes, segmentation, and predicting the future from static images. This tutorial introduces the intuitions behind VAEs, explains the mathematics behind them, and describes some empirical behavior. No prior knowledge of variational Bayesian methods is assumed.
2014
- (Rezendeimenez et al., 2014) ⇒ Danilo J. Rezendeimenez, Shakir Mohamed, and Daan Wierstra. (2014). “Stochastic Backpropagation and Approximate Inference in Deep Generative Models.” In: Proceedings of the 31st International Conference on Machine Learning (ICML-2014).
- ABSTRACT: We marry ideas from deep neural networks and approximate Bayesian inference to derive a generalised class of deep, directed generative models, endowed with a new algorithm for scalable inference and learning. Our algorithm introduces a recognition model to represent approximate posterior distributions, and that acts as a stochastic encoder of the data. We develop stochastic back-propagation -- rules for back-propagation through stochastic variables -- and use this to develop an algorithm that allows for joint optimisation of the parameters of both the generative and recognition model. We demonstrate on several real-world data sets that the model generates realistic samples, provides accurate imputations of missing data and is a useful tool for high-dimensional data visualisation.
2013
- (Kingma & Welling, 2013) ⇒ Diederik P. Kingma, and Max Welling. (2013). “Auto-encoding Variational Bayes.” arXiv preprint arXiv:1312.6114
- ABSTRACT: How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets? We introduce a stochastic variational inference and learning algorithm that scales to large datasets and, under some mild differentiability conditions, even works in the intractable case. Our contributions is two-fold. First, we show that a reparameterization of the variational lower bound yields a lower bound estimator that can be straightforwardly optimized using standard stochastic gradient methods. Second, we show that for i.i.d. datasets with continuous latent variables per datapoint, posterior inference can be made especially efficient by fitting an approximate inference model (also called a recognition model) to the intractable posterior using the proposed lower bound estimator. Theoretical advantages are reflected in experimental results.