HMM Network Instance
(Redirected from Viterbi lattice)
Jump to navigation
Jump to search
An HMM network instance is a lattice-based directed conditional probability network that abides by a hidden Markov network metamodel.
- AKA: Hidden Markov Model, Hidden Markov Graph, Viterbi Lattice.
- Context:
- It can (typically) be composed of:
- It can be associated to Hidden Markov Metamodel.
- It can be a Finite-State Sequence Tagging Model.
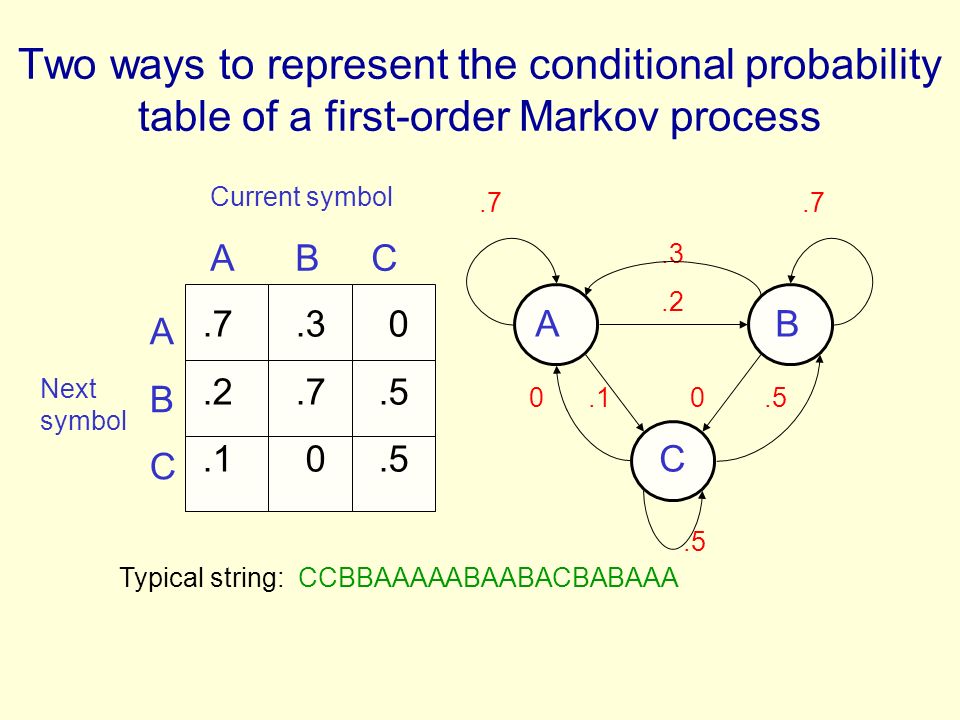
- It can be represented with:
- It can be produced by a Hidden Markov Modeling System (that applies an HMM training algorithm to solve an HMM training task)
- Example(s):
- Counter-Example(s):
- See: Undirected Probabilistic Network.
References
2005
- (Cohen & Hersh, 2005) ⇒ Aaron Michael Cohen, and William R. Hersh. (2005). “A Survey of Current Work in Biomedical Text Mining.” In: Briefings in Bioinformatics 2005 6(1). doi:10.1093/bib/6.1.57
- Zhou et al. trained a hidden Markov model (HMM) on a set of features based on
2004
- http://www.cassandra.org/pomdp/pomdp-faq.shtml
- Michael Littman's nifty explanatory grid:
| Markov Models |
Do we have control over the state transitons? |
||
|---|---|---|---|
| NO | YES | ||
| Are the states completely observable? |
YES | Markov Chain |
MDPMarkov Decision Process |
| NO | HMMHidden Markov Model |
POMDPPartially ObservableMarkov Decision Process |
|
1997
- (Shin, Han et al., 1995) ⇒ Joong-Ho Shin, Young-Soek Han, and Key-Sun Choi. (1995). “A HMM Part-of-Speech Tagger for Korean with wordphrasal Relations". In: Proceedings of Recent Advances in Natural Language Processing (RANLP 1995)
- QUOTE: The trained hidden Markov network reflecting both morpheme and word-phrase relations contains 712 nodes and 28553 edges.
1993
- (Tanaka et al., 1993) ⇒ H. Tanaka & al. (1993). “Classification of Proteins via Successive State Splitting of Hidden Markov Network.” In: ProceedingsW26 in IJCAI93,