Mean Reciprocal Rank (MRR) Measure
(Redirected from MRR (mean reciprocal rank))
Jump to navigation
Jump to search
A Mean Reciprocal Rank (MRR) Measure is an average measure of reciprocal ranks over a set of listed results.
- Context:
- It can be represented as [math]\displaystyle{ \text{MRR} = \frac{1}{|Q|} \sum_{i=1}^{|Q|} \frac{1}{\text{rank}_i}. \! }[/math].
- It can (often) be a Ranking Performance Measure.
- It can be implemented in a MRR Library.
- It is a reciprocal value of a harmonic mean of the ranks.
- …
- Example(s):
ir-evaluation-py.mrr- a Python's implementation,- …
- Counter-Example(s):
- See: Harmonic Mean, Multiplicative Inverse, Information Retrieval Task, Discounted Cumulative Gain, Mean Average Precision, Softmax Cross Entropy.
References
2020
- (Wikipedia, 2020) ⇒ https://en.wikipedia.org/wiki/Mean_reciprocal_rank Retrieved:2020-9-18.
- The mean reciprocal rank is a statistic measure for evaluating any process that produces a list of possible responses to a sample of queries, ordered by probability of correctness. The reciprocal rank of a query response is the multiplicative inverse of the rank of the first correct answer: 1 for first place, for second place, for third place and so on. The mean reciprocal rank is the average of the reciprocal ranks of results for a sample of queries Q:
[math]\displaystyle{ \text{MRR} = \frac{1}{|Q|} \sum_{i=1}^{|Q|} \frac{1}{\text{rank}_i}. \! }[/math]
where [math]\displaystyle{ \text{rank}_i }[/math] refers to the rank position of the first relevant document for the i-th query.
The reciprocal value of the mean reciprocal rank corresponds to the harmonic mean of the ranks.
- The mean reciprocal rank is a statistic measure for evaluating any process that produces a list of possible responses to a sample of queries, ordered by probability of correctness. The reciprocal rank of a query response is the multiplicative inverse of the rank of the first correct answer: 1 for first place, for second place, for third place and so on. The mean reciprocal rank is the average of the reciprocal ranks of results for a sample of queries Q:
2019a
- (Taifi, 2019) ⇒ Moussa Taifi. (2019). “MRR vs MAP vs NDCG: Rank-Aware Evaluation Metrics And When To Use Them." In: Medium (2019-11-25)
- QUOTE: ... MRR: Mean Reciprocal Rank - This is the simplest metric of the three. It tries to measure “Where is the first relevant item?”. It is closely linked to the binary relevance family of metrics. The algorithm goes as follows: ...
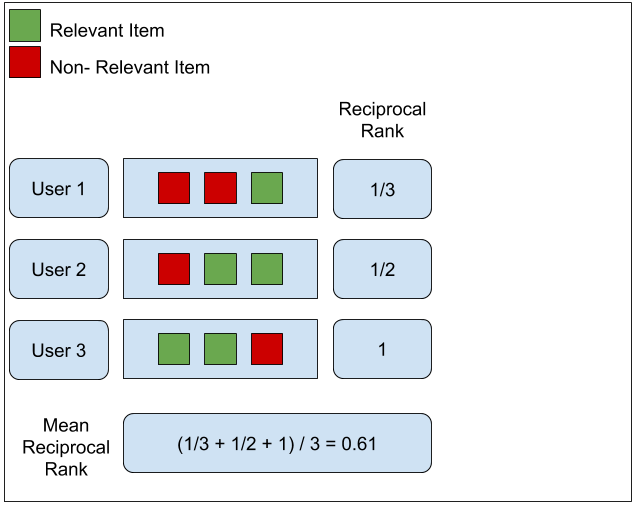
- QUOTE: ... MRR: Mean Reciprocal Rank - This is the simplest metric of the three. It tries to measure “Where is the first relevant item?”. It is closely linked to the binary relevance family of metrics. The algorithm goes as follows: ...
2019b
- (Le, 2019) ⇒ Duc-Trong Le. (2019). “Finding Relevant Files for Bug Reports Based on Mean Reciprocal Rank Maximization Approach.” Springer,
2019c
- (Bruch et al., 2019) ⇒ Sebastian Bruch, Xuanhui Wang, Michael Bendersky, and Marc Najork. (2019). “An Analysis of the Softmax Cross Entropy Loss for Learning-to-rank with Binary Relevance.” In: Proceedings of the 2019 ACM SIGIR International Conference on Theory of Information Retrieval, pp. 75-78.
- ABSTRACT: One of the challenges of learning-to-rank for information retrieval is that ranking metrics are not smooth and as such cannot be optimized directly with gradient descent optimization methods. This gap has given rise to a large body of research that reformulates the problem to fit into existing machine learning frameworks or defines a surrogate, ranking-appropriate loss function. One such loss is ListNet's which measures the cross entropy between a distribution over documents obtained from scores and another from ground-truth labels. This loss was designed to capture permutation probabilities and as such is considered to be only loosely related to ranking metrics. In this work, however, we show that the above statement is not entirely accurate. In fact, we establish an analytical connection between ListNet's loss and two popular ranking metrics in a learning-to-rank setup with binary relevance labels. In particular, we show that the loss bounds Mean Reciprocal Rank and Normalized Discounted Cumulative Gain. Our analysis sheds light on ListNet's behavior and explains its superior performance on binary labeled data over data with graded relevance.
- QUOTE: ... While the softmax cross entropy loss is seemingly disconnected from ranking metrics, in this work we prove that there indeed exists a link between the two concepts under certain conditions. In particular, we show that softmax cross entropy is a bound on Mean Reciprocal Rank (MRR) as well as NDCG when working with binary ground-truth labels. We hope the analysis presented in thiswork furthers our collective understanding of this loss function andexplains its behavior in the presence of binary relevance labels ...
- Reciprocal Rank is only considers the position of the first relevant document and is generally appropriate for evaluations on click logs. The metric is computed as follows:
- RR(πf(x),y)=max{i|yi>0}1πf(x)(i).(4)
- In practice, given an evaluation set
- Q={(x,y)}and a metric M, we are interested in the mean metric:
- M(πf(x),y)=1|Q|Õ(x,y)∈QM(πf(x),y
- … In fact, we establish an analytical connection between ListNet’s loss and two popular ranking metrics in a learning-to-rank setup with binary relevance labels. In particular, we show that the loss bounds Mean Reciprocal Rank and Normalized Discounted Cumulative Gain.
2009d
- (Craswell, 2009) ⇒ Nick Craswell (2009). “Mean Reciprocal Rank". In: Encyclopedia of Database Systems - MMR.
- QUOTE: The Reciprocal Rank (RR) information retrieval measure calculates the reciprocal of the rank at which the first relevant document was retrieved. RR is 1 if a relevant document was retrieved at rank 1, if not it is 0.5 if a relevant document was retrieved at rank 2 and so on. When averaged across queries, the measure is called the Mean Reciprocal Rank (MRR).