Location Test

A Location Test is a statistical hypothesis test that compares the location parameter of a statistical population to a given constant, or that compares the location parameters of two statistical populations to each other.

• Context:
  • It can range from being a One-Sample Location Test to being a Two-Sample Location Test to being ...
  • It can range from being a Parametric Location Test to being a Nonparametric Location Test.
  • It can range from being a Paired Location Test to being an Independent Location Test.
  • It can range from being an Ordinal Location Test to being a Nominal Location Test.
• Example(s):
  • a Welch's t-Test.
• See: Location Parameter, Statistical Population, Expected Value.

---

---

References

2016

• (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/location_test Retrieved:2016-9-14.
  • A location test is a statistical hypothesis test that compares the location parameter of a statistical population to a given constant, or that compares the location parameters of two statistical populations to each other. Most commonly, the location parameter (or parameters) of interest are expected values, but location tests based on medians or other measures of location are also used.

• https://en.wikipedia.org/w/index.php?title=Location_test&action=edit&section=3
  • The following table summarizes some common parametric and nonparametric tests for the means of one or more samples.

Ordinal and numerical measures

1 group		N ≥ 30		One-sample t-test
		N < 30	Normally distributed	One-sample t-test
			Not normal	Sign test
2 groups	Independent	N ≥ 30		t-test
		N < 30	Normally distributed	t-test
			Not normal	Mann–Whitney U or Wilcoxon rank-sum test
	Paired	N ≥ 30		paired t-test
		N < 30	Normally distributed	paired t-test
			Not normal	Wilcoxon signed-rank test
3 or more groups	Independent	Normally distributed	1 factor	One way anova
			≥ 2 factors	two or other anova
		Not normal		Kruskal–Wallis one-way analysis of variance by ranks
	Dependent	Normally distributed		Repeated measures anova
		Not normal		Friedman two-way analysis of variance by ranks

Nominal measures

1 group		np and n(1-p) ≥ 5	Z-approximation
		np or n(1-p) < 5	binomial
2 groups	Independent	np < 5	fisher exact test
		np ≥ 5	chi-squared test
	Paired		McNemar or Kappa
3 or more groups	Independent	np < 5	collapse categories for chi-squared test
		np ≥ 5	chi-squared test
	Dependent		Cochran´s Q

2010

• http://www.psychology.emory.edu/clinical/bliwise/Tutorials/CHTESTS/choose/nom.htm
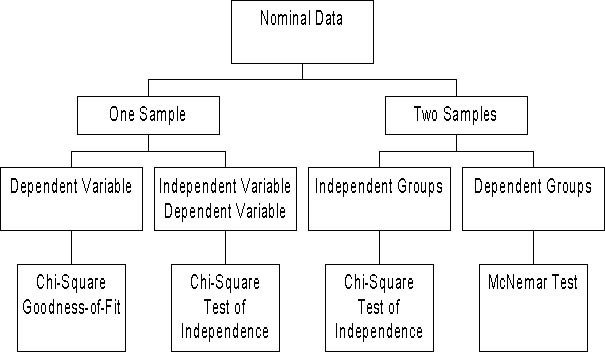
  • QUOTE: The following tests can be used with nominal data. Which test you select is determined by the number of samples and whether you are testing an hypothesis about group differences or the association between independent and dependent variables. If you are testing an hypothesis about group differences, you also must consider whether the groups/samples are independent or dependent
    

---