Statistical Hypothesis Testing Task
A Statistical Hypothesis Testing Task is a statistical inference task for testing two opposing statistical hypotheses about a statistical population using data from samples.
- AKA: Confirmatory Data Analysis, Hypothesis Test.
- Context:
- input:
- Input Data:
- [math]\displaystyle{ \{(x_1,y_1,z_1,...)(x_2,y_2,z_2,...),\cdots, (x_n,y_n,z_n,...)\} }[/math], a sample drawn from a Univariate, Bivariate or Multivariate Probability Distribution.
Data type: Parametric samples are composed by ratio or interval data while non-parametric samples are composed nominal or ordinal data type.
Datasets Relationship: Two or more samples can be independent measures, repeated-measures or matched-pair measures.
- [math]\displaystyle{ \{(x_1,y_1,z_1,...)(x_2,y_2,z_2,...),\cdots, (x_n,y_n,z_n,...)\} }[/math], a sample drawn from a Univariate, Bivariate or Multivariate Probability Distribution.
- Input Parameters:
- [math]\displaystyle{ \alpha }[/math], a significance level with values vary between 0 and 1 is required for the decision rule method.
- [math]\displaystyle{ \theta }[/math], Statistical Significance Measure (e.g. parametric statistical measures) required one or more hypothesized population parameters (e.g. hypothesized population means, population variances values).
- Input Data:
- output:
- Test Statistic value,
- P-value or Region of Acceptance.
- Region of Rejection (optional)
- Decision Errors (optional).
- requirements:
- Null Hypothesis ([math]\displaystyle{ H_0 }[/math]) and Alternative Hypothesis ([math]\displaystyle{ H_A }[/math]) are defined such that they are mutually exclusive.
- A Test Statistic defined by a parametric statistical test or non-parametric statistical test.
- Decision Rules which will reject or fail to reject the null hypothesis given the significance level and test statistic. These decision rules can be described according to a selected approach: P-value or region of acceptance approach.
- ...
- It can range from being a Non-Parametric Statistical Test to a Parametric Statistical Test.
- It can range from being Univariate Hypothesis Testing, Bivariate Hypothesis Testing, to being Multivariate Hypothesis Testing.
- It can be solved by a Statistical Hypothesis Testing System (that implements a statistical hypothesis testing algorithm).
- It can involve a Controlled Group and a Treatment Group.
- ...
- input:
- Example(s):
- Group Comparison Tests, such as:
- Mean Difference Tests, such as:
- Two Sample T-Test comparing group means.
- One Sample T-Test comparing against reference value.
- Paired Sample T-Test comparing matched observations.
- Median Difference Tests, such as:
- Mean Difference Tests, such as:
- Distribution Tests, such as:
- Goodness of Fit Tests, such as:
- Independence Tests, such as:
- Variance Tests, such as:
- Analysis of Variance Tests, such as:
- One-Way ANOVA for single factor comparison.
- Two-Way ANOVA for multiple factors.
- Repeated Measures ANOVA for longitudinal data.
- Variance Homogeneity Tests, such as:
- Analysis of Variance Tests, such as:
- Correlation Tests, such as:
- Linear Correlation Tests, such as:
- Association Tests, such as:
- Regression Model Tests, such as:
- Linear Regression Tests, such as:
- Model Fit Tests, such as:
- F-Test for overall model significance.
- T-Test for coefficient significance.
- R-Squared Test for model fit.
- …
- Group Comparison Tests, such as:
- Counter-Example(s):
- See: Statistical Hypothesis, Location Test, Bayesian Inference, Benferroni Correction, Fisher Score, Statistical Significance Measure, Scientific Method, Two-Tailed Test.
References
2017a
- (Changing Works, 2017) ⇒ Retrieved on 2017-05-07 from http://changingminds.org/explanations/research/analysis/parametric_non-parametric.htm Copyright: Changing Works 2002-2016
- There are two types of test data and consequently different types of analysis. As the table below shows, parametric data has an underlying normal distribution which allows for more conclusions to be drawn as the shape can be mathematically described. Anything else is non-parametric.
Parametric Statistical Tests Non-Parametric Statistical Tests Assumed distribution Normally Distributed Any Assumed variance Homogeneous Any Typical data Ratio or Interval Ordinal or Nominal Data set relationships Independent Any Usual central measure Mean Median Benefits Can draw more conclusions Simplicity; Less affected by outliers
2017b
- (Jim Frost, 2015) ⇒ Retrieved on 2017-05-07 from http://blog.minitab.com/blog/adventures-in-statistics-2/choosing-between-a-nonparametric-test-and-a-parametric-test Copyright ©2017 Minitab Inc. All rights Reserved.
- Nonparametric tests are like a parallel universe to parametric tests. The table shows related pairs of hypothesis tests that Minitab statistical software offers.
Parametric tests (means) Nonparametric tests (medians) 1-sample t test 1-sample Sign, 1-sample Wilcoxon 2-sample t test Mann-Whitney test One-Way ANOVA Kruskal-Wallis, Mood’s median test Factorial DOE with one factor and one blocking variable Friedman test
2017c
- (Surbhi, 2016) ⇒ Retrived on 2017-05-07 from http://keydifferences.com/difference-between-parametric-and-nonparametric-test.html Copyright © 2017 KeyDifferences
PARAMETRIC TEST NON-PARAMETRIC TEST Independent Sample t Test Mann-Whitney test Paired samples t test Wilcoxon signed Rank test One way Analysis of Variance (ANOVA) Kruskal Wallis Test One way repeated measures Analysis of Variance Friedman's ANOVA
2016A
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/Statistical_hypothesis_testing Retrieved:2016-5-24.
- A statistical hypothesis is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables. A statistical hypothesis test is a method of statistical inference. Commonly, two statistical data sets are compared, or a data set obtained by sampling is compared against a synthetic data set from an idealized model. A hypothesis is proposed for the statistical relationship between the two data sets, and this is compared as an alternative to an idealized null hypothesis that proposes no relationship between two data sets. The comparison is deemed statistically significant if the relationship between the data sets would be an unlikely realization of the null hypothesis according to a threshold probability—the significance level. Hypothesis tests are used in determining what outcomes of a study would lead to a rejection of the null hypothesis for a pre-specified level of significance. The process of distinguishing between the null hypothesis and the alternative hypothesis is aided by identifying two conceptual types of errors (type 1 & type 2), and by specifying parametric limits on e.g. how much type 1 error will be permitted. An alternative framework for statistical hypothesis testing is to specify a set of statistical models, one for each candidate hypothesis, and then use model selection techniques to choose the most appropriate model. The most common selection techniques are based on either Akaike information criterion or Bayes factor.
Statistical hypothesis testing is sometimes called confirmatory data analysis. It can be contrasted with exploratory data analysis, which may not have pre-specified hypotheses.
- A statistical hypothesis is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables. A statistical hypothesis test is a method of statistical inference. Commonly, two statistical data sets are compared, or a data set obtained by sampling is compared against a synthetic data set from an idealized model. A hypothesis is proposed for the statistical relationship between the two data sets, and this is compared as an alternative to an idealized null hypothesis that proposes no relationship between two data sets. The comparison is deemed statistically significant if the relationship between the data sets would be an unlikely realization of the null hypothesis according to a threshold probability—the significance level. Hypothesis tests are used in determining what outcomes of a study would lead to a rejection of the null hypothesis for a pre-specified level of significance. The process of distinguishing between the null hypothesis and the alternative hypothesis is aided by identifying two conceptual types of errors (type 1 & type 2), and by specifying parametric limits on e.g. how much type 1 error will be permitted. An alternative framework for statistical hypothesis testing is to specify a set of statistical models, one for each candidate hypothesis, and then use model selection techniques to choose the most appropriate model. The most common selection techniques are based on either Akaike information criterion or Bayes factor.
2016B
- (Minitab, 2016) ⇒ http://support.minitab.com/en-us/minitab/17/topic-library/basic-statistics-and-graphs/hypothesis-tests/basics/what-is-a-hypothesis-test/
- A hypothesis test is a statistical test that is used to determine whether there is enough evidence in a sample of data to infer that a certain condition is true for the entire population.
- A hypothesis test examines two opposing hypotheses about a population: the null hypothesis and the alternative hypothesis. The null hypothesis is the statement being tested. Usually the null hypothesis is a statement of "no effect" or "no difference". The alternative hypothesis is the statement you want to be able to conclude is true.
- Based on the sample data, the test determines whether to reject the null hypothesis. You use a p-value, to make the determination. If the p-value is less than or equal to the level of significance, which is a cut-off point that you define, then you can reject the null hypothesis.
- A common misconception is that statistical hypothesis tests are designed to select the more likely of two hypotheses. Instead, a test will remain with the null hypothesis until there is enough evidence (data) to support the alternative hypothesis.
- Examples of questions you can answer with a hypothesis test include:
- Does the mean height of undergraduate women differ from 66 inches?
- Is the standard deviation of their height equal less than 5 inches?
- Do male and female undergraduates differ in height?
2016C
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/Location_test#Parametric_and_nonparametric_location_tests
- The following table summarizes some common parametric and nonparametric tests for the means of one or more samples.
Ordinal and numerical measures 1 group N ≥ 30 One-sample t-test N < 30 Normally distributed One-sample t-test Not normal Sign test 2 groups Independent N ≥ 30 t-test N < 30 Normally distributed t-test Not normal Mann–Whitney U or Wilcoxon rank-sum test Paired N ≥ 30 paired t-test N < 30 Normally distributed paired t-test Not normal Wilcoxon signed-rank test 3 or more groups Independent Normally distributed 1 factor One way anova ≥ 2 factors two or other anova Not normal Kruskal–Wallis one-way analysis of variance by ranks Dependent Normally distributed Repeated measures anova Not normal Friedman two-way analysis of variance by ranks
Nominal measures 1 group np and n(1-p) ≥ 5 Z-approximation np or n(1-p) < 5 binomial 2 groups Independent np < 5 fisher exact test np ≥ 5 chi-squared test Paired McNemar or Kappa 3 or more groups Independent np < 5 collapse categories for chi-squared test np ≥ 5 chi-squared test Dependent Cochran´s Q
2012
- Eric W. Weisstein. “Hypothesis Testing." From MathWorld -- A Wolfram Web Resource. http://mathworld.wolfram.com/HypothesisTesting.html
- Hypothesis testing is the use of statistics to determine the probability that a given hypothesis is true. The usual process of hypothesis testing consists of four steps.
- Formulate the null hypothesis [math]\displaystyle{ H_0 }[/math] (commonly, that the observations are the result of pure chance) and the alternative hypothesis [math]\displaystyle{ H_a }[/math] (commonly, that the observations show a real effect combined with a component of chance variation).
- Identify a test statistic that can be used to assess the truth of the null hypothesis.
- Compute the P-value, which is the probability that a test statistic at least as significant as the one observed would be obtained assuming that the null hypothesis were true. The smaller the P-value, the stronger the evidence against the null hypothesis.
- Compare the p-value to an acceptable significance value alpha (sometimes called an alpha value). If p<=alpha, that the observed effect is statistically significant, the null hypothesis is ruled out, and the alternative hypothesis is valid.
- Hypothesis testing is the use of statistics to determine the probability that a given hypothesis is true. The usual process of hypothesis testing consists of four steps.
2010
- (Siegfried, 2010) ⇒ Tom Siegfried. (2010). “Are, Its Wrong: Science fails to face the shortcomings of statistics.” In: Science News, 177(7).
- http://www.psychology.emory.edu/clinical/bliwise/Tutorials/CHTESTS/choose/nom.htm
- QUOTE: The following tests can be used with nominal data. Which test you select is determined by the number of samples and whether you are testing an hypothesis about group differences or the association between independent and dependent variables. If you are testing an hypothesis about group differences, you also must consider whether the groups/samples are independent or dependent
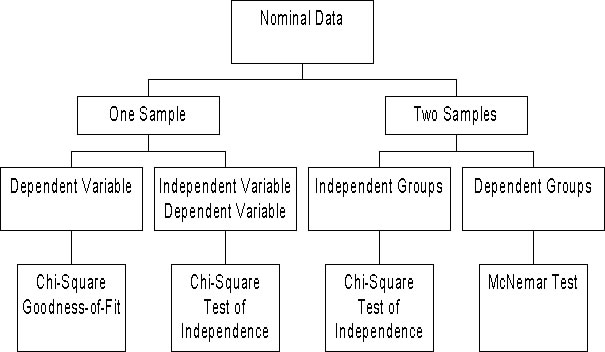
- QUOTE: The following tests can be used with nominal data. Which test you select is determined by the number of samples and whether you are testing an hypothesis about group differences or the association between independent and dependent variables. If you are testing an hypothesis about group differences, you also must consider whether the groups/samples are independent or dependent
2006
- (Dubnicka, 2006k) ⇒ Suzanne R. Dubnicka. (2006). “Introduction to Statistics - Handout 11." Kansas State University, Introduction to Probability and Statistics I, STAT 510 - Fall 2006.
- QUOTE: ... Estimation and hypothesis testing are the two common forms of statistical inference. ... In hypothesis testing, we are trying to answer a yes/no question regarding the parameter of interest. For example, we might want ask, “Is the parameter larger than a specified value?” Hypothesis testing often uses the point estimate and its standard error to answer the question of interest?
2003
- http://www.nature.com/nrg/journal/v4/n9/glossary/nrg1155_glossary.html
- QUOTE: ... A test statistic is a statistic that is used in a statistical test to discriminate between two competing hypotheses, the so-called null and alternative hypotheses.
1991
- (Efron & Tibshirani, 1991) ⇒ Bradley Efron, and Robert Tibshirani. (1991). “Statistical Data Analysis in the Computer Age.” In: Science, 253(5018). 10.1126/science.253.5018.390
- QUOTE: Most of our familiar statistical methods, such as hypothesis testing, linear regression, analysis of variance, and maximum likelihood estimation, were designed to be implemented on mechanical calculators. ...
1960
- (Wason, 1960) ⇒ Peter C. Wason. (1960). “On the Failure to Eliminate Hypotheses in a Conceptual Task." Quarterly journal of experimental psychology 12, no. 3 doi:10.1080/17470216008416717
- QUOTE: This investigation examines the extent to which intelligent young adults seek (i) confirming evidence alone (enumerative induction) or (ii) confirming and discontinuing evidence (eliminative induction), in order to draw conclusions in a simple conceptual task. The experiment is designed so that use of confirming evidence alone will almost certainly lead to erroneous conclusions because (i) the correct concept is entailed by many more obvious ones, and (ii) the universe of possible instances (numbers) is infinite.
Six out of 29 subjects reached the correct conclusion without previous incorrect ones, 13 reached one incorrect conclusion, nine reached two or more incorrect conclusions, and one reached no conclusion. The results showed that those subjects, who reached two or more incorrect conclusions, were unable, or unwilling to test their hypotheses. The implications are discussed in relation to scientific thinking.
- QUOTE: This investigation examines the extent to which intelligent young adults seek (i) confirming evidence alone (enumerative induction) or (ii) confirming and discontinuing evidence (eliminative induction), in order to draw conclusions in a simple conceptual task. The experiment is designed so that use of confirming evidence alone will almost certainly lead to erroneous conclusions because (i) the correct concept is entailed by many more obvious ones, and (ii) the universe of possible instances (numbers) is infinite.