Huffman Coding Algorithm
(Redirected from Huffman coding)
Jump to navigation
Jump to search
A Huffman Coding Algorithm is a lossless compression algorithm that creates a (variable-length coding) Huffman tree.
- Context:
- It can be applied by a Huffman Coding System (to solve a Huffman coding task).
- Example(s):
- Counter-Example(s):
- See: Prefix Code, Entropy Encoding, Text Compression, Variable-Length Code, Linear Time, Weighted Path Length From The Root, Expected Value.
References
2015
- (Wikipedia, 2015) ⇒ http://en.wikipedia.org/wiki/Huffman_coding Retrieved:2015-2-3.
- In computer science and information theory, a Huffman code is an optimal prefix code found using the algorithm developed by David A. Huffman while he was a Ph.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes". The process of finding and/or using such a code is called Huffman coding and is a common technique in entropy encoding, including in lossless data compression. The algorithm's output can be viewed as a variable-length code table for encoding a source symbol (such as a character in a file). Huffman's algorithm derives this table based on the estimated probability or frequency of occurrence (weight) for each possible value of the source symbol. As in other entropy encoding methods, more common symbols are generally represented using fewer bits than less common symbols. Huffman's method can be efficiently implemented, finding a code in linear time to the number of input weights if these weights are sorted. However, although optimal among methods encoding symbols separately, Huffman coding is not always optimal among all compression methods.
- (Wikipedia, 2015) ⇒ http://en.wikipedia.org/wiki/Huffman_coding#Informal_description Retrieved:2015-2-3.
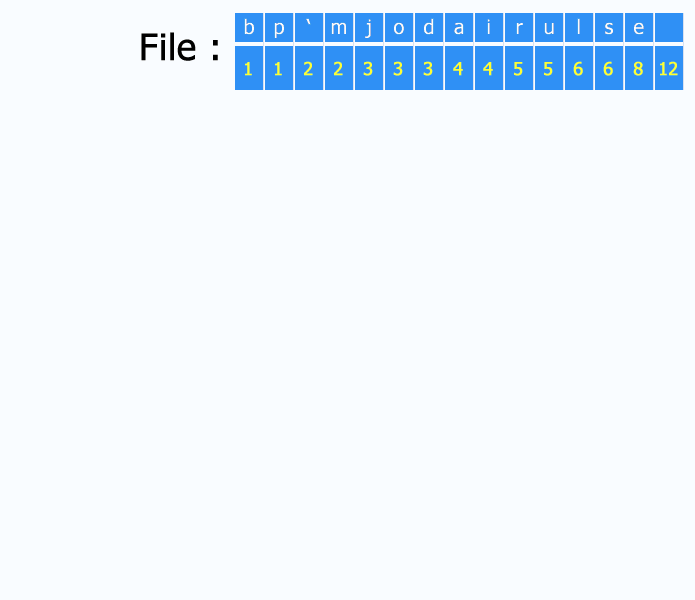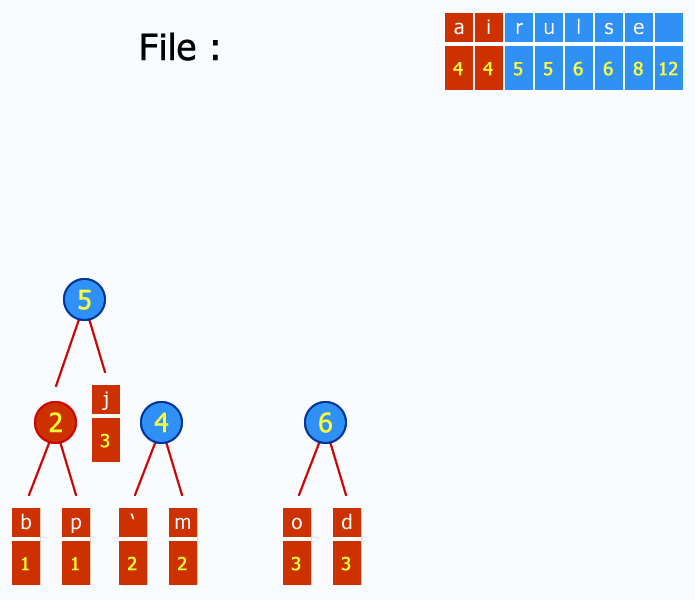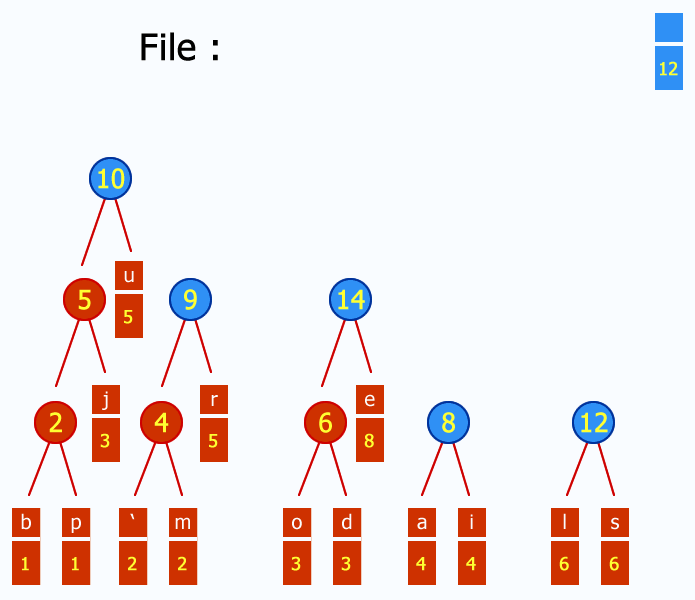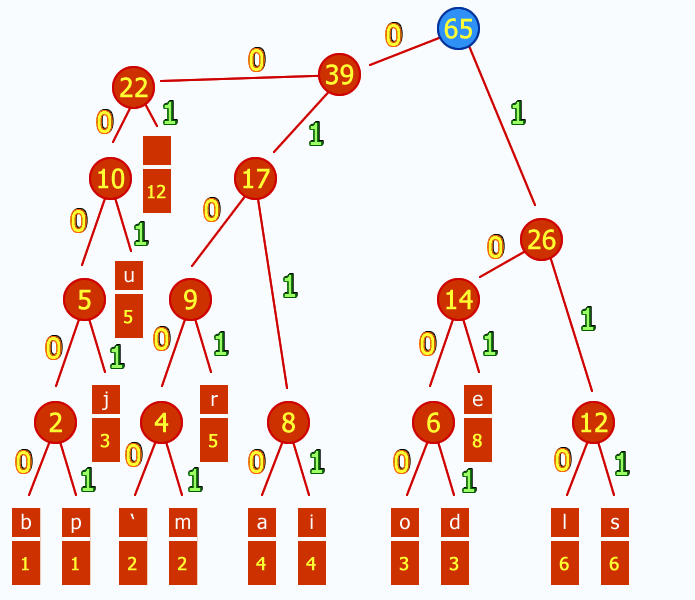
- Given: A set of symbols and their weights (usually proportional to probabilities).
- Find: A prefix-free binary code (a set of codewords) with minimum expected codeword length (equivalently, a tree with minimum weighted path length from the root).