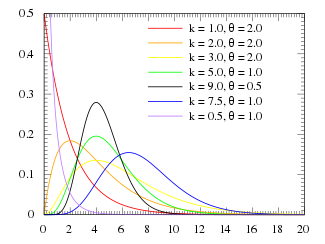
Gamma Probability Distribution Family
A Gamma Probability Distribution Family is a two-parameter family of continuous probability distributions (of gamma density functions).
- Example(s):
- Counter-Example(s):
- See: Scale Parameter, Digamma Function, Trigamma Function, Rate Parameter, Poisson Distribution, Maximum Entropy Probability Distribution, Shape Parameter, Exponential Distribution, Chi-Squared Distribution.
References
- http://www.google.com/images?q=gamma+probability+distribution
- http://www.mathworks.com/help/toolbox/stats/gampdf.html
- https://upload.wikimedia.org/wikipedia/commons/thumb/e/e6/Gamma_distribution_pdf.svg/325px-Gamma_distribution_pdf.svg.png
2022
- (Wikipedia, 2022) ⇒ https://en.wikipedia.org/wiki/Gamma_distribution#Occurrence_and_applications Retrieved:2022-9-24.
- Consider a sequence of events, with the waiting time for each event being an exponential distribution with rate [math]\displaystyle{ \beta }[/math] . Then the waiting time for the [math]\displaystyle{ n }[/math] -th event to occur is the gamma distribution with integer shape [math]\displaystyle{ \alpha = n }[/math] . This construction of the gamma distribution allows it to model a wide variety of phenomena where several sub-events, each taking time with exponential distribution, must happen in sequence for a major event to occur. Examples include the waiting time of cell-division events, number of compensatory mutations for a given mutation, waiting time until a repair is necessary for a hydraulic system, and so on. The gamma distribution has been used to model the size of insurance claims [1] and rainfalls. This means that aggregate insurance claims and the amount of rainfall accumulated in a reservoir are modelled by a gamma process – much like the exponential distribution generates a Poisson process. The gamma distribution is also used to model errors in multi-level Poisson regression models, because a mixture of Poisson distributions with gamma distributed rates has a known closed form distribution, called negative binomial. In wireless communication, the gamma distribution is used to model the multi-path fading of signal power;see also Rayleigh distribution and Rician distribution. In oncology, the age distribution of cancer incidence often follows the gamma distribution, whereas the shape and scale parameters predict, respectively, the number of driver events and the time interval between them. In neuroscience, the gamma distribution is often used to describe the distribution of inter-spike intervals.[2] [3] In bacterial gene expression, the copy number of a constitutively expressed protein often follows the gamma distribution, where the scale and shape parameter are, respectively, the mean number of bursts per cell cycle and the mean number of protein molecules produced by a single mRNA during its lifetime.[4] In genomics, the gamma distribution was applied in peak calling step (i.e. in recognition of signal) in ChIP-chip[5] and ChIP-seq[6] data analysis.
The gamma distribution is widely used as a conjugate prior in Bayesian statistics. It is the conjugate prior for the precision (i.e. inverse of the variance) of a normal distribution. It is also the conjugate prior for the exponential distribution.
- Consider a sequence of events, with the waiting time for each event being an exponential distribution with rate [math]\displaystyle{ \beta }[/math] . Then the waiting time for the [math]\displaystyle{ n }[/math] -th event to occur is the gamma distribution with integer shape [math]\displaystyle{ \alpha = n }[/math] . This construction of the gamma distribution allows it to model a wide variety of phenomena where several sub-events, each taking time with exponential distribution, must happen in sequence for a major event to occur. Examples include the waiting time of cell-division events, number of compensatory mutations for a given mutation, waiting time until a repair is necessary for a hydraulic system, and so on. The gamma distribution has been used to model the size of insurance claims [1] and rainfalls. This means that aggregate insurance claims and the amount of rainfall accumulated in a reservoir are modelled by a gamma process – much like the exponential distribution generates a Poisson process. The gamma distribution is also used to model errors in multi-level Poisson regression models, because a mixture of Poisson distributions with gamma distributed rates has a known closed form distribution, called negative binomial. In wireless communication, the gamma distribution is used to model the multi-path fading of signal power;see also Rayleigh distribution and Rician distribution. In oncology, the age distribution of cancer incidence often follows the gamma distribution, whereas the shape and scale parameters predict, respectively, the number of driver events and the time interval between them. In neuroscience, the gamma distribution is often used to describe the distribution of inter-spike intervals.[2] [3] In bacterial gene expression, the copy number of a constitutively expressed protein often follows the gamma distribution, where the scale and shape parameter are, respectively, the mean number of bursts per cell cycle and the mean number of protein molecules produced by a single mRNA during its lifetime.[4] In genomics, the gamma distribution was applied in peak calling step (i.e. in recognition of signal) in ChIP-chip[5] and ChIP-seq[6] data analysis.
2015
- (Wikipedia, 2015) ⇒ http://en.wikipedia.org/wiki/gamma_distribution Retrieved:2015-6-24.
- In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The common exponential distribution and chi-squared distribution are special cases of the gamma distribution. There are three different parametrizations in common use:
- With a shape parameter k and a scale parameter θ.
- With a shape parameter α = k and an inverse scale parameter β = 1/θ, called a rate parameter.
- With a shape parameter k and a mean parameter μ = k/β.
- In each of these three forms, both parameters are positive real numbers.
The parameterization with k and θ appears to be more common in econometrics and certain other applied fields, where e.g. the gamma distribution is frequently used to model waiting times. For instance, in life testing, the waiting time until death is a random variable that is frequently modeled with a gamma distribution. [7] The parameterization with α and β is more common in Bayesian statistics, where the gamma distribution is used as a conjugate prior distribution for various types of inverse scale (aka rate) parameters, such as the λ of an exponential distribution or a Poisson distribution [8] – or for that matter, the β of the gamma distribution itself. (The closely related inverse gamma distribution is used as a conjugate prior for scale parameters, such as the variance of a normal distribution.) If k is an integer, then the distribution represents an Erlang distribution; i.e., the sum of k independent exponentially distributed random variables, each of which has a mean of θ (which is equivalent to a rate parameter of 1/θ). The gamma distribution is the maximum entropy probability distribution for a random variable X for which E[X] = kθ = α/β is fixed and greater than zero, and E[ln(X)] = ψ(k) + ln(θ) = ψ(α) − ln(β) is fixed (ψ is the digamma function).
- In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The common exponential distribution and chi-squared distribution are special cases of the gamma distribution. There are three different parametrizations in common use:
- ↑ p. 43, Philip J. Boland, Statistical and Probabilistic Methods in Actuarial Science, Chapman & Hall CRC 2007
- ↑ J. G. Robson and J. B. Troy, "Nature of the maintained discharge of Q, X, and Y retinal ganglion cells of the cat", J. Opt. Soc. Am. A 4, 2301–2307 (1987)
- ↑ M.C.M. Wright, I.M. Winter, J.J. Forster, S. Bleeck "Response to best-frequency tone bursts in the ventral cochlear nucleus is governed by ordered inter-spike interval statistics", Hearing Research 317 (2014)
- ↑ N. Friedman, L. Cai and X. S. Xie (2006) "Linking stochastic dynamics to population distribution: An analytical framework of gene expression", Phys. Rev. Lett. 97, 168302.
- ↑ DJ Reiss, MT Facciotti and NS Baliga (2008) "Model-based deconvolution of genome-wide DNA binding", Bioinformatics, 24, 396–403
- ↑ MA Mendoza-Parra, M Nowicka, W Van Gool, H Gronemeyer (2013) "Characterising ChIP-seq binding patterns by model-based peak shape deconvolution", BMC Genomics, 14:834
- ↑ See Hogg and Craig (1978, Remark 3.3.1) for an explicit motivation
- ↑ Scalable Recommendation with Poisson Factorization, Prem Gopalan, Jake M. Hofman, David Blei, arXiv.org 2014
2006
- (Dubnicka, 2006g) ⇒ Suzanne R. Dubnicka. (2006). “Special Continuous Distributions - Handout 7." Kansas State University, Introduction to Probability and Statistics I, STAT 510 - Fall 2006.
- THE GAMMA FUNCTION: The gamma function is a function of t, defined for all k > 0 as ...
- TERMINOLOGY : A random variable X is said to have a gamma distribution with parameters k > 0 and > 0 if its pdf is given by fX(x) =
- …
- 0, otherwise.
- TERMINOLOGY : In the Gamma(k, ) family, when k = /2, for any integer , and = 1/2, we call the resulting distribution a 2 distribution with degrees of freedom. If X has a 2 distribution with degrees of freedom, we write X ∼ 2().
2004
- (Arsham, 2004) ⇒ Hossein Arsham. (2004). “Topics in Statistical Data Analysis: Revealing Facts From Data." Webpage
- Application: A basic distribution of statistics for variables bounded at one side - for example [math]\displaystyle{ x }[/math] greater than or equal to zero. Gives distribution of time required for exactly k independent events to occur, assuming events take place at a constant rate. Used frequently in queuing theory, reliability, and other industrial applications.
- Example: Distribution of time between re-calibrations of instrument that needs re calibration after k uses; time between inventory restocking, time to failure for a system with standby components.
- Comments: Erlangian, exponential, and chi-square distributions are special cases. The Dirichlet is a multidimensional extension of the Beta distribution.
- Distribution of a product of iid uniform (0, 1) random? Like many problems with products, this becomes a familiar problem when turned into a problem about sums. If X is uniform (for simplicity of notation make it U(0,1)), Y=-log(X) is exponentially distributed, so the log of the product of X1, X2, … Xn is the sum of Y1, Y2, … Yn which has a gamma (scaled chi-square) distribution. Thus, it is a gamma density with shape parameter n and scale 1.