Fully-Connected Neural Network Layer
(Redirected from Fully Connected NN Layer)
A Fully-Connected Neural Network Layer is a Neural Network Layer in which every artificial neuron(or graph node) form a fully-connected network with those of the adjancet layers but not with those within the same layer.
- AKA: FCNNL, Fully-Connected NN Layer, Fully-Connected Artificial Neural Network Layer.
- Context:
- It can be any layer in a Fully-Connected Neural Network.
- Example(s):
- Counter-Example(s):
- A Single Neural Network Layer.
- Partially Connected Neural Network Layers such as
- A Neural Network Layer in which artificial neurons are connected within the layer such as
- See: Artificial Neural Network, Directed Graph, Feed-Forward Neural Network, Perceptron.
References
2017a
- (Miikkulainen, 2017) ⇒ Miikkulainen R. (2017) "Topology of a Neural Network". In: Sammut, C., Webb, G.I. (eds) "Encyclopedia of Machine Learning and Data Mining". Springer, Boston, MA
- ABSTRACT: Topology of a neural network refers to the way the neurons are connected, and it is an important factor in how the network functions and learns. A common topology in unsupervised learning is a direct mapping of inputs to a collection of units that represents categories (e.g., Self-Organizing Maps). The most common topology in supervised learning is the fully connected, three-layer, feedforward network (see Backpropagation and Radial Basis Function Networks): All input values to the network are connected to all neurons in the hidden layer (hidden because they are not visible in the input or output), the outputs of the hidden neurons are connected to all neurons in the output layer, and the activations of the output neurons constitute the output of the whole network. Such networks are popular partly because they are known theoretically to be universal function approximators (with, e.g., a sigmoid or Gaussian nonlinearity in the hidden layer neurons), although networks with more layers may be easier to train in practice (e.g., Cascade-Correlation).
2017b
- (CS231n, 2017) ⇒ http://cs231n.github.io/neural-networks-1/#layers Retrieved: 2017-12-31
- QUOTE: Neural Networks as neurons in graphs. Neural Networks are modeled as collections of neurons that are connected in an acyclic graph. In other words, the outputs of some neurons can become inputs to other neurons. Cycles are not allowed since that would imply an infinite loop in the forward pass of a network. Instead of an amorphous blobs of connected neurons, Neural Network models are often organized into distinct layers of neurons. For regular neural networks, the most common layer type is the fully-connected layer in which neurons between two adjacent layers are fully pairwise connected, but neurons within a single layer share no connections. Below are two example Neural Network topologies that use a stack of fully-connected layers:
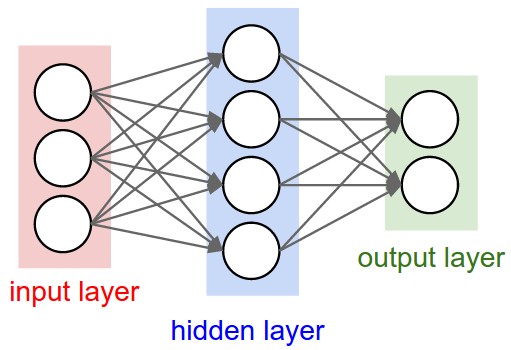
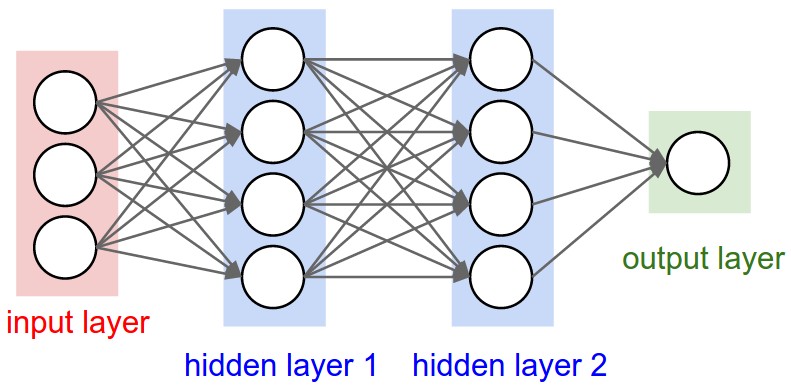 Left: A 2-layer Neural Network (one hidden layer of 4 neurons (or units) and one output layer with 2 neurons), and three inputs. Right: A 3-layer neural network with three inputs, two hidden layers of 4 neurons each and one output layer. Notice that in both cases there are connections (synapses) between neurons across layers, but not within a layer.
Left: A 2-layer Neural Network (one hidden layer of 4 neurons (or units) and one output layer with 2 neurons), and three inputs. Right: A 3-layer neural network with three inputs, two hidden layers of 4 neurons each and one output layer. Notice that in both cases there are connections (synapses) between neurons across layers, but not within a layer.
2017c
- (Wikipedia, 2017) ⇒ https://en.wikipedia.org/wiki/Network_topology#Fully_connected_network Retrieved:2017-12-17.
- In a fully connected network, all nodes are interconnected. (In graph theory this is called a complete graph.) The simplest fully connected network is a two-node network. A fully connected network doesn't need to use packet switching or broadcasting. However, since the number of connections grows quadratically with the number of nodes: This kind of topology does not trip and affect other nodes in the network [math]\displaystyle{ c= \frac{n(n-1)}{2}.\, }[/math] This makes it impractical for large networks.


