Fat-Tailed Distribution
(Redirected from Fat-tailed distribution)
Jump to navigation
Jump to search
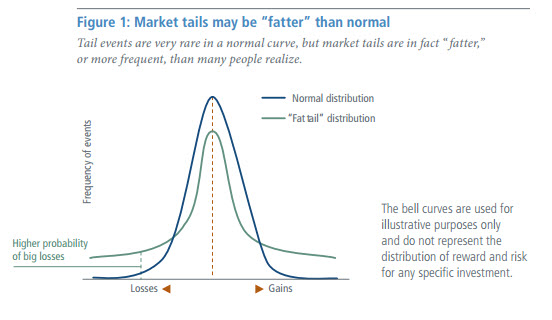
A Fat-Tailed Distribution is a heavy-tailed probability distribution with large skewness or kurtosis.
- Context:
- It can range from being a Right Fat-Tailed Distribution to being a Left Fat-Tailed Distribution.
- It can (often) be used to model a Fat-Tailed Dataset (in which moderately extreme outcomes to be more likely than would be normally expected).
- Example(s):
- Counter-Example(s):
- See: Probability Distribution, Heavy-Tailed Distribution, Skewness, Kurtosis, Normal Distribution, Exponential Distribution, Power Law.
References
2016
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/fat-tailed_distribution Retrieved:2016-9-11.
- A fat-tailed distribution is a probability distribution that has the property, along with the other heavy-tailed distributions, that it exhibits large skewness or kurtosis. This comparison is often made relative to the normal distribution, or to the exponential distribution. Fat-tailed distributions have been empirically encountered in a variety of areas: economics, physics, and earth sciences. Some fat-tailed distributions have power law decay in the tail of the distribution, but do not necessarily follow a power law everywhere.
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/heavy-tailed_distribution#Definition_of_heavy-tailed_distribution Retrieved:2016-9-11.
- The distribution of a random variable X with distribution function F is said to have a heavy right tail if : [math]\displaystyle{ \lim_{x \to \infty} e^{\lambda x}\Pr[X\gt x] = \infty \quad \mbox{for all } \lambda\gt 0.\, }[/math] This is also written in terms of the tail distribution function : [math]\displaystyle{ \overline{F}(x) \equiv \Pr[X\gt x] \, }[/math] as : [math]\displaystyle{ \lim_{x \to \infty} e^{\lambda x}\overline{F}(x) = \infty \quad \mbox{for all } \lambda\gt 0.\, }[/math] This is equivalent to the statement that the moment generating function of F, MF(t), is infinite for all t > 0. [1]
The definitions of heavy-tailed for left-tailed or two tailed distributions are similar.
- The distribution of a random variable X with distribution function F is said to have a heavy right tail if : [math]\displaystyle{ \lim_{x \to \infty} e^{\lambda x}\Pr[X\gt x] = \infty \quad \mbox{for all } \lambda\gt 0.\, }[/math] This is also written in terms of the tail distribution function : [math]\displaystyle{ \overline{F}(x) \equiv \Pr[X\gt x] \, }[/math] as : [math]\displaystyle{ \lim_{x \to \infty} e^{\lambda x}\overline{F}(x) = \infty \quad \mbox{for all } \lambda\gt 0.\, }[/math] This is equivalent to the statement that the moment generating function of F, MF(t), is infinite for all t > 0. [1]
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/fat-tailed_distribution#Definition Retrieved:2016-9-11.
- The distribution of a random variable X is said to have a fat tail if : [math]\displaystyle{ \Pr[X\gt x] \sim x^{- \alpha}\text{ as }x \to \infty,\qquad \alpha \gt 0.\, }[/math] That is, if X has probability density function [math]\displaystyle{ f_X(x) }[/math] , : [math]\displaystyle{ f_X(x) \sim x^{ - (1 + \alpha)} \text{ as }x \to \infty, \qquad \alpha \gt 0.\, }[/math] Here the tilde notation " [math]\displaystyle{ \sim }[/math] " refers to the asymptotic equivalence of functions.
2014
- (Babbar et al., 2014) ⇒ Rohit Babbar, Cornelia Metzig, Ioannis Partalas, Eric Gaussier, and Massih-Reza Amini. (2014). “On Power Law Distributions in Large-scale Taxonomies.” In: ACM SIGKDD Explorations Newsletter Journal, 16(1). doi:10.1145/2674026.2674033
- QUOTE: In many of the large-scale physical and social complex systems phenomena fat-tailed distributions occur, for which different generating mechanisms have been proposed. …
… In the context of designing classifiers for large-scale taxonomies, which automatically assign unseen documents to leaf-level categories, we highlight how the fat-tailed nature of these distributions can be leveraged to analytically study the space complexity of such classifiers.
- QUOTE: In many of the large-scale physical and social complex systems phenomena fat-tailed distributions occur, for which different generating mechanisms have been proposed. …
2012
- ↑ Rolski, Schmidli, Scmidt, Teugels, Stochastic Processes for Insurance and Finance, 1999