Bidirectional Recurrent Neural Network (BiRNN) Training System
A Bidirectional Recurrent Neural Network (BiRNN) Training System is a Recurrent Neural Network Training System that implements a BRNN Forward Pass Algorithm and a BRNN Backward Pass Algorithm (to create a BiRNN).
- Context:
- It implements a BRNN training algorithm to produce a Bidirectional Recurrent Neural Network.
- …
- Example(s):
- Counter-Example(s):
- See: Bidirectional LSTM (biLSTM) Network, LSTM Training System, RNN Training System, Artificial Neural Network, PyTorch, LSTM Unit, BiLSTM Network, ConvNet Network, RNN Network.
References
2018a
- (Github, 2018) ⇒ Theano-Recurrence Training System: https://github.com/uyaseen/theano-recurrence#training Retrieved: 2018-07-01
train.pyprovides a convenient methodtrain(..)to train each model, you can select the recurrent model with therec_modelparameter, it is set togruby default (possible options includernn,gru,lstm,birnn,bigru&bilstm), number of hidden neurons in each layer (at the moment only single layer models are supported to keep the things simple, although adding more layers is very trivial) can be adjusted byn_hparameter intrain(..), which by default is set to100. As the model is trained it stores the current best state of the model i.e set of weights (best = least training error), the stored model is in thedata\models\MODEL-NAME-best_model.pkl, also this stored model can later be used for resuming training from the last point or just for prediction/sampling. If you don't want to start training from scratch and instead use the already trained model then setuse_existing_model=Truein argument totrain(..). Also optimization strategies can be specified totrain(..)via optimizer parameter, currently supported optimizations arermsprop,adamandvanilla stochastic gradient descentand can be found inutilities\optimizers.py.b_path,learning_rate,n_epochsin thetrain(..)specifies the'base path to store model' (default = data\models\),'initial learning rateof the optimizer', and 'number of epochs respectively'. During the training some logs (current epoch, sample, cross-entropy error etc) are shown on console to get an idea of how well learning is proceeding, logging frequencycan be specified vialogging_freqin thetrain(..). At the end of training, a plot ofcross-entropy error vs # of iterationsgives an overview of overall training process and is also stored in theb_path.
2018b
- (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Bidirectional_recurrent_neural_networks Retrieved:2018-7-1.
- Bidirectional Recurrent Neural Networks (BRNN) were invented in 1997 by Schuster and Paliwal. BRNNs were introduced to increase the amount of input information available to the network. For example, multilayer perceptron (MLPs) and time delay neural network (TDNNs) have limitations on the input data flexibility, as they require their input data to be fixed. Standard recurrent neural network (RNNs) also have restrictions as the future input information cannot be reached from the current state. On the contrary, BRNNs do not require their input data to be fixed. Moreover, their future input information is reachable from the current state. The basic idea of BRNNs is to connect two hidden layers of opposite directions to the same output. By this structure, the output layer can get information from past and future states.
BRNN are especially useful when the context of the input is needed. For example, in handwriting recognition, the performance can be enhanced by knowledge of the letters located before and after the current letter.
- Bidirectional Recurrent Neural Networks (BRNN) were invented in 1997 by Schuster and Paliwal. BRNNs were introduced to increase the amount of input information available to the network. For example, multilayer perceptron (MLPs) and time delay neural network (TDNNs) have limitations on the input data flexibility, as they require their input data to be fixed. Standard recurrent neural network (RNNs) also have restrictions as the future input information cannot be reached from the current state. On the contrary, BRNNs do not require their input data to be fixed. Moreover, their future input information is reachable from the current state. The basic idea of BRNNs is to connect two hidden layers of opposite directions to the same output. By this structure, the output layer can get information from past and future states.
2018c
- (Cui, Ke & Wang, 2018) ⇒ Zhiyong Cui, Ruimin Ke, and Yinhai Wang (2018). "Deep Bidirectional and Unidirectional LSTM Recurrent Neural Network for Network-wide Traffic Speed Prediction" (PDF). arXiv preprint [arXiv:1801.02143].
- QUOTE: The idea of BDLSTMs comes from bidirectional RNN (Schuster & Paliwal, 1997), which processes sequence data in both forward and backward directions with two separate hidden layers. BDLSTMs connect the two hidden layers to the same output layer. It has been proved that the bidirectional networks are substantially better than unidirectional ones in many fields, like phoneme classification (Graves & Schmidhuber, 2005) and speech recognition (Graves, Jaitly, & Mohamed, 2013).
(...) the structure of an unfolded BDLSTM layer, containing a forward LSTM layer and a backward LSTM layer, is introduced and illustrated in Fig. 3.
- QUOTE: The idea of BDLSTMs comes from bidirectional RNN (Schuster & Paliwal, 1997), which processes sequence data in both forward and backward directions with two separate hidden layers. BDLSTMs connect the two hidden layers to the same output layer. It has been proved that the bidirectional networks are substantially better than unidirectional ones in many fields, like phoneme classification (Graves & Schmidhuber, 2005) and speech recognition (Graves, Jaitly, & Mohamed, 2013).
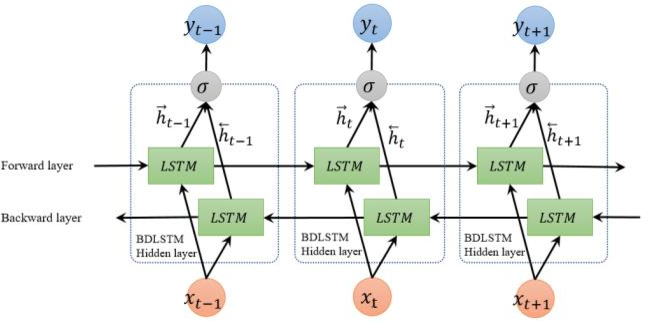
Fig. 3 Unfolded architecture of bidirectional LSTM with three consecutive steps
2017
- (Schmidhuber, 2017) ⇒ Schmidhuber, J. (2017) "Deep Learning". In: Sammut, C., Webb, G.I. (eds) "Encyclopedia of Machine Learning and Data Mining". Springer, Boston, MA
- QUOTE: .... Recursive NNs (Goller and Küchler 1996) generalize RNNs, by operating on hierarchical structures, recursively combining child representations into parent representations. Bidirectional RNNs (BRNNs) (Schuster and Paliwal 1997) are designed for input sequences whose starts and ends are known in advance, such as spoken sentences to be labeled by their phonemes. DAG-RNNs (Baldi and Pollastri 2003) generalize BRNNs to multiple dimensions. Recursive NNs, BRNNs, and DAG-RNNs unfold their full potential when combined with LSTM (Graves et al. 2009).
2015
- (Fan et al., 2015) ⇒ Bo Fan, Lijuan Wang, Frank K. Soong, and Lei Xie (2015, April). "Photo-real talking head with deep bidirectional LSTM". In Acoustics, Speech and Signal Processing (ICASSP), 2015 IEEE International Conference on (pp. 4884-4888). IEEE. DOI: 10.1109/ICASSP.2015.7178899
- QUOTE: In our BLSTM network, as shown in Fig. 3, label sequence [math]\displaystyle{ L }[/math] is the input layer, and visual feature sequence [math]\displaystyle{ V }[/math] serves as the output layer and [math]\displaystyle{ H }[/math] denotes the hidden layer. In particular, at t-th frame, the input of the network is the t-th label vector [math]\displaystyle{ l_t }[/math] and the output is the [math]\displaystyle{ t }[/math]-th visual feature vector [math]\displaystyle{ v_t }[/math]. As described in (Graves, 2012), the basic idea of this bidirectional structure is to present each sequence forwards and backwards to two separate recurrent hidden layers, both of which are connected to the same output layer. This provides the network with complete, symmetrical, past and future context for every point in the input sequence. Please note that in Fig. 3, more hidden layers can be added in to construct a deep BLSTM.
In the training stage, we have multiple sequence pairs of [math]\displaystyle{ L }[/math] and [math]\displaystyle{ V }[/math]. As we represent both sequences as continuous numerical vectors, the network is treated as a regression model to minimizing the SSE of predicting [math]\displaystyle{ \hat{V} }[/math] from [math]\displaystyle{ L }[/math].

Fig. 3. BLSTM neural network in our talking head system.
- QUOTE: In our BLSTM network, as shown in Fig. 3, label sequence [math]\displaystyle{ L }[/math] is the input layer, and visual feature sequence [math]\displaystyle{ V }[/math] serves as the output layer and [math]\displaystyle{ H }[/math] denotes the hidden layer. In particular, at t-th frame, the input of the network is the t-th label vector [math]\displaystyle{ l_t }[/math] and the output is the [math]\displaystyle{ t }[/math]-th visual feature vector [math]\displaystyle{ v_t }[/math]. As described in (Graves, 2012), the basic idea of this bidirectional structure is to present each sequence forwards and backwards to two separate recurrent hidden layers, both of which are connected to the same output layer. This provides the network with complete, symmetrical, past and future context for every point in the input sequence. Please note that in Fig. 3, more hidden layers can be added in to construct a deep BLSTM.
2008
- (Graves, 2008) ⇒ Alex Graves (2008). "Supervised Sequence Labelling with Recurrent Neural Networks", PhD Thesis.
- QUOTE: (...)In this thesis we find that BRNNs consistently outperform unidirectional RNNs on real-world sequence labelling tasks.
The forward pass for the BRNN hidden layers is the same as for a unidirectional RNN, except that the input sequence is presented in opposite directions to the two hidden layers, and the output layer is not updated until both hidden layers have processed the entire input sequence:
- QUOTE: (...)In this thesis we find that BRNNs consistently outperform unidirectional RNNs on real-world sequence labelling tasks.
Do forward pass for the forward hidden layer, storing activations at each timestep
for t = T to 1 do
Do forward pass for the backward hidden layer, storing activations at each timestep
for' t = 1 to T do Do forward pass for the output layer, using the stored activations from both hidden layers
- Similarly, the backward pass proceeds as for a standard RNN trained with BPTT, except that all the output layer δ terms are calculated first, then fed back to the two hidden layers in opposite directions:
Do BPTT backward pass for the output layer only, storing δ terms at each timestep
for t = T to 1 do
Do BPTT backward pass for the forward hidden layer, using the stored δ terms from the output layer
for' t = 1 to T do Do BPTT backward pass for the backward hidden layer, using the stored δ terms from the output layer
2005a
- (Graves & Schmidhuber, 2005) ⇒ Alex Graves and Jurgen Schmidhuber (2005). "Framewise phoneme classification with bidirectional LSTM and other neural network architectures" (PDF). Neural Networks, 18(5-6), 602-610. DOI 10.1016/j.neunet.2005.06.042
- QUOTE: The basic idea of bidirectional recurrent neural nets (BRNNs) (Schuster & Paliwal, 1997; Baldi et al., 1999) is to present each training sequence forwards and backwards to two separate recurrent nets, both of which are connected to the same output layer. (In some cases a third network is used in place of the output layer, but here we have used the simpler model). This means that for every point in a given sequence, the BRNN has complete, sequential information about all points before and after it.
2005b
- (Graves, Fernandez & Schmidhuber, 2005) ⇒ Alex Graves, Santiago Fernandez, and Jurgen Schmidhuber (2005). "Bidirectional LSTM networks for improved phoneme classification and recognition" (PDF). In: Proceedings of The International Conference on Artificial Neural Networks.
- QUOTE: For example, when classifying a frame of speech data, it helps to look at the frames after it as well as those before — especially if it occurs near the end of a word or segment. In general, recurrent neural networks (RNNs) are well suited to such tasks, where the range of contextual effects is not known in advance. However they do have some limitations: firstly, since they process inputs in temporal order, their outputs tend to be mostly based on previous context; secondly they have trouble learning time-dependencies more than a few timesteps long (Hochreiter, 2001). An elegant solution to the first problem is provided by bidirectional networks (Schuster & Paliwal, 1997; Baldi et al., 1999). In this model, the input is presented forwards and backwards to two separate recurrent nets, both of which are connected to the same output layer.
1999
- (Baldi et al., 1999) ⇒ Pierre Baldi, Soren Brunak, Paolo Frasconi, Giovanni Soda, and Gianluca Pollastri (1999). "Exploiting the past and the future in protein secondary structure prediction" (PDF) . Bioinformatics, 15(11), 937-946. DOI: 10.1093/bioinformatics/15.11.937
- QUOTE: ... all the NNs have a single hidden layer. The hidden state [math]\displaystyle{ F_t }[/math] is copied back to the input. This is graphically represented in Fig. 2 using the causal shift operator [math]\displaystyle{ q^{-1} }[/math] that operates on a generic temporal variable [math]\displaystyle{ X_t }[/math] and is symbolically defined as [math]\displaystyle{ X_{t-1} = q^{-1}X_t }[/math]. Similarly, [math]\displaystyle{ q }[/math], the inverse (or non-causal) shift operator is defined [math]\displaystyle{ X_{t+1} = qX_t }[/math] and [math]\displaystyle{ q^{-11} q = 1 }[/math]. As shown in Fig. 2, a non-causal copy is performed on the hidden state [math]\displaystyle{ B_t }[/math]. Clearly, removal of [math]\displaystyle{ \{B_t\} }[/math] would result in a standard causal RNN.

Figure 2: A BRNN architecture.
- QUOTE: ... all the NNs have a single hidden layer. The hidden state [math]\displaystyle{ F_t }[/math] is copied back to the input. This is graphically represented in Fig. 2 using the causal shift operator [math]\displaystyle{ q^{-1} }[/math] that operates on a generic temporal variable [math]\displaystyle{ X_t }[/math] and is symbolically defined as [math]\displaystyle{ X_{t-1} = q^{-1}X_t }[/math]. Similarly, [math]\displaystyle{ q }[/math], the inverse (or non-causal) shift operator is defined [math]\displaystyle{ X_{t+1} = qX_t }[/math] and [math]\displaystyle{ q^{-11} q = 1 }[/math]. As shown in Fig. 2, a non-causal copy is performed on the hidden state [math]\displaystyle{ B_t }[/math]. Clearly, removal of [math]\displaystyle{ \{B_t\} }[/math] would result in a standard causal RNN.
1997
- (Schuster & Paliwal, 1997) ⇒ Mike Schuster, and Kuldip K. Paliwal. (1997). “Bidirectional Recurrent Neural Networks.” In: IEEE Transactions on Signal Processing Journal, 45(11). doi:10.1109/78.650093
- QUOTE: To overcome the limitations of a regular RNN outlined in the previous section, we propose a bidirectional recurrent neural network (BRNN) that can be trained using all available input information in the past and future of a specific time frame.
1) Structure: The idea is to split the state neurons of a regular RNN in a part that is responsible for the positive time direction (forward states) and a part for the negative time direction (backward states). Outputs from forward states are not connected to inputs of backward states, and vice versa. This leads to the general structure that can be seen in Fig. 3, where it is unfolded over three time steps.
.
Fig. 3. General structure of the bidirectional recurrent neural network (BRNN) shown unfolded in time for three time steps
- QUOTE: To overcome the limitations of a regular RNN outlined in the previous section, we propose a bidirectional recurrent neural network (BRNN) that can be trained using all available input information in the past and future of a specific time frame.