Bias Variance Decomposition
A Bias Variance Decomposition is a Bias-variance Tradeoff for estimating a learning algorithm's expected generalization error.
- Example(s):
- Counter-Example(s):
- See: Bagging Algorithm, Novel Applications, Model Validation, Cross-Validation, Regularization, Feature Selection, Hyperparameter Optimization.
References
2018
- (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Bias–variance_tradeoff Retrieved:2018-4-8.
- In statistics and machine learning, the bias–variance tradeoff (or dilemma) is the problem of simultaneously minimizing two sources of error that prevent supervised learning algorithms from generalizing beyond their training set:* The bias is an error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting).
- The variance is an error from sensitivity to small fluctuations in the training set. High variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs (overfitting).
- The bias–variance decomposition is a way of analyzing a learning algorithm's expected generalization error with respect to a particular problem as a sum of three terms, the bias, variance, and a quantity called the irreducible error, resulting from noise in the problem itself.
This tradeoff applies to all forms of supervised learning: classification, regression (function fitting),[1] [2] and structured output learning. It has also been invoked to explain the effectiveness of heuristics in human learning.[3]
- In statistics and machine learning, the bias–variance tradeoff (or dilemma) is the problem of simultaneously minimizing two sources of error that prevent supervised learning algorithms from generalizing beyond their training set:* The bias is an error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting).
2017
- (Sammut & Webb, 2017) ⇒ (2017) Bias Variance Decomposition. In: Sammut, C., Webb, G.I. (eds) Encyclopedia of Machine Learning and Data Mining. Springer, Boston, MA
- QUOTE: The bias-variance decomposition is a useful theoretical tool to understand the performance characteristics of a learning algorithm. The following discussion is restricted to the use of squared loss as the performance measure, although similar analyses have been undertaken for other loss functions. The case receiving most attention is the zero-one loss (i.e., classification problems), in which case the decomposition is nonunique and a topic of active research. See Domingos (1992) for details.
The decomposition allows us to see that the mean squared error of a model (generated by a particular learning algorithm) is in fact made up of two components. The bias component tells us how accurate the model is, on average across different possible training sets. The variance component tells us how sensitive the learning algorithm is to small changes in the training set
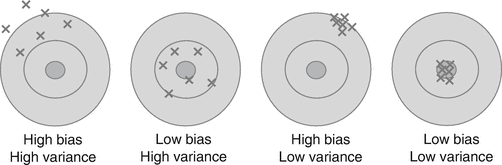 Fig. 1: Bias Variance Decomposition,
Fig. 1: Bias Variance Decomposition, The bias-variance decomposition is like trying to hit the bullseye on a dartboard. Each dart is thrown after training our “dart-throwing” model in a slightly different manner. If the darts vary wildly, the learner is high variance. If they are far from the bullseye, the learner is high bias. The ideal is clearly to have both low bias and low variance; however this is often difficult, giving an alternative terminology as the bias-variance “dilemma” (Dartboard analogy, Moore and McCabe 2002)
Mathematically, this can be quantified as a decomposition of the mean squared error function. For a testing example, [math]\displaystyle{ \{\mathbf{x},d\} }[/math], the decomposition is:
[math]\displaystyle{ \begin{array}{rcl} \mathcal{E}_{\mathcal{D}}\{(f(\mathbf{x}) - d)^{2}\}& =& (\mathcal{E}_{ \mathcal{D}}\{f(\mathbf{x})\} - d)^{2} {}\\ & & + \mathcal{E}_{\mathcal{D}}\{(f(\mathbf{x}) -\mathcal{E}_{\mathcal{D}}\{f(\mathbf{x})\})^{2}\}, {}\\ \mathrm{MSE}& =& \mathrm{bias}^{2} +\mathrm{ variance}, {}\\ \end{array} }[/math]
where the expectations are with respect to all possible training sets. In practice, this can be estimated by cross-validation over a single finite training set, enabling a deeper understanding of the algorithm characteristics. For example, efforts to reduce variance often cause increases in bias, and vice versa. A large bias and low variance is an indicator that a learning algorithm is prone to overfitting the model.
- QUOTE: The bias-variance decomposition is a useful theoretical tool to understand the performance characteristics of a learning algorithm. The following discussion is restricted to the use of squared loss as the performance measure, although similar analyses have been undertaken for other loss functions. The case receiving most attention is the zero-one loss (i.e., classification problems), in which case the decomposition is nonunique and a topic of active research. See Domingos (1992) for details.
- ↑ Geman, Stuart; E. Bienenstock; R. Doursat (1992). "Neural networks and the bias/variance dilemma" (PDF). Neural Computation. 4: 1–58. doi:10.1162/neco.1992.4.1.1.
- ↑ Bias–variance decomposition, In Encyclopedia of Machine Learning. Eds. Claude Sammut, Geoffrey I. Webb. Springer 2011. pp. 100-101
- ↑ Gigerenzer, Gerd; Brighton, Henry (2009). “Homo Heuristicus: Why Biased Minds Make Better Inferences". Topics in Cognitive Science. 1: 107–143. doi:10.1111/j.1756-8765.2008.01006.x. PMID 25164802.